Logistic-Regression Calibration for Forensic Text Comparison: A Data-Driven Framework for Validating Likelihood Ratios

Abstract

This article provides a comprehensive guide for researchers and forensic professionals on the application of logistic-regression calibration in forensic text comparison (FTC). It covers the foundational Likelihood Ratio (LR) framework essential for scientifically defensible evidence evaluation, details the step-by-step methodology for converting similarity scores to calibrated LRs, and addresses key challenges like data scarcity and topic mismatch. The content further explores advanced optimization techniques and underscores the critical importance of empirical validation under casework-relevant conditions, synthesizing these elements to present a robust, transparent, and legally sound approach for forensic authorship analysis.

The Likelihood Ratio Framework: A Logical Foundation for Forensic Text Comparison

Definition and Core Concept of the Likelihood Ratio

The Likelihood Ratio (LR) is a fundamental statistical measure for evaluating the strength of forensic evidence. It is defined as the ratio of two probabilities of observing the same evidence under two competing hypotheses. In the context of forensic science, these are typically the prosecution's hypothesis (Hp) and the defense's hypothesis (Hd) [1].

The formal expression of the LR is: LR = P(E|Hp) / P(E|Hd) Where:

• P(E|Hp) is the probability of observing the evidence (E) given that the prosecution's hypothesis is true
• P(E|Hd) is the probability of observing the evidence (E) given that the defense's hypothesis is true [1]

The LR provides a balanced framework for interpreting evidence, with values interpreted as follows:

• LR > 1: The evidence provides more support for Hp
• LR = 1: The evidence provides equal support for both hypotheses (neutral evidence)
• LR < 1: The evidence provides more support for Hd [1]

The LR in Forensic Text Comparison

In forensic text comparison (FTC), the LR framework is used to evaluate the strength of linguistic evidence. The application of LR in FTC requires empirical validation under conditions that replicate casework scenarios using relevant data [2]. Without proper validation that accounts for specific case conditions such as topic mismatches, the trier-of-fact may be misled in their final decision [2].

The Dirichlet-multinomial model, followed by logistic regression calibration, has been demonstrated as a viable method for calculating LRs in FTC research. This approach allows for the quantification of the strength of evidence while accounting for the complexities of textual data [2].

Quantitative Interpretation of Likelihood Ratios

The numerical value of the LR can be translated into verbal equivalents to facilitate interpretation. These verbal scales serve as guides for communicating the strength of evidence, though they should be applied with caution [1].

Table 1: Verbal Equivalents for Likelihood Ratio Values

Strength of Evidence	Likelihood Ratio Range
Limited support	LR < 1 to 10
Moderate evidence	LR 10 to 100
Moderately strong evidence	LR 100 to 1000
Strong evidence	LR 1000 to 10000
Very strong evidence	LR > 10000

[1]

Calibration Protocols for Forensic Text Comparison

Experimental Setup for LR Validation

To ensure the validity of LR systems in FTC, research must replicate casework conditions using relevant data. The following protocol outlines key steps for empirical validation:

• Define Relevant Conditions: Identify textual features and conditions pertinent to the case under investigation (e.g., topic, register, style).
• Data Collection: Compile text samples that reflect these conditions, ensuring appropriate representation of both same-author and different-author scenarios.
• Model Training: Implement a Dirichlet-multinomial model to calculate initial LR values.
• Logistic Regression Calibration: Apply logistic regression to calibrate the raw LR outputs, improving their evidential reliability.
• Performance Assessment: Evaluate the calibrated LRs using the log-likelihood-ratio cost (Cllr) and visualize results with Tippett plots [2].

Critical Considerations for Meaningful LRs

For an LR to be meaningful in casework, the validation data must reflect:

• Individual Examiner Performance: Data should be representative of the particular examiner performing the analysis, as performance varies between practitioners [3].
• Case-Specific Conditions: Test materials must reflect the specific conditions of the case (e.g., text type, quality, linguistic features) [3].
• Adequate Sample Size: Sufficient same-source and different-source test trials are required for robust model training [3].

Uncertainty Assessment in Likelihood Ratios

The calculation of LRs involves subjective choices in model selection and assumptions. To address this, an uncertainty pyramid framework should be employed, exploring the range of LR values attainable under different reasonable models [4]. This is particularly critical in FTC, where methodological choices can significantly impact results.

The lattice of assumptions approach provides a structured method for assessing how different modeling decisions affect final LR values, offering transparency about the uncertainty inherent in any specific LR calculation [4].

Research Reagent Solutions for FTC Studies

Table 2: Essential Materials and Methodological Components for Forensic Text Comparison Research

Research Component	Function/Description
Dirichlet-Multinomial Model	Statistical model for calculating initial likelihood ratios from text data [2]
Logistic Regression Calibration	Method for calibrating raw LR outputs to improve reliability and interpretability [2]
Log-Likelihood-Ratio Cost (Cllr)	Performance metric for evaluating the accuracy and discrimination of a forensic evaluation system [2] [3]
Tippett Plots	Graphical method for visualizing the distribution of LRs for same-source and different-source comparisons [2]
Pool-Adjacent-Violators (PAV) Algorithm	Non-parametric algorithm used for calibrating likelihood-ratio values [5]
Black-Box Studies	Experimental designs where ground truth is known to researchers but not participants, used to estimate error rates [4] [3]

Workflow Diagram for LR Calculation and Calibration

The following diagram illustrates the logical workflow for calculating and calibrating likelihood ratios in forensic text comparison research:

The Likelihood Ratio (LR) framework is increasingly established as the logically and legally correct method for the evaluation of forensic evidence, including that derived from text [6] [7]. An LR quantifies the strength of evidence by comparing the probability of observing the evidence under two competing hypotheses: the prosecution hypothesis (Hp) and the defense hypothesis (Hd) [6]. In the context of Forensic Text Comparison (FTC), P(E|Hp) represents the similarity component—the probability of the observed linguistic evidence if the suspect is the author. Conversely, P(E|Hd) represents the typicality component—the probability of that same evidence if some other person from a relevant population is the author [6]. The proper calibration of these LRs, often using logistic regression, is critical to ensuring that the reported strengths of evidence are reliable and meaningful for the trier-of-fact [2] [7]. This document outlines the application of these principles, with a focus on protocols for validation and calibration within FTC research.

Theoretical Foundation of Similarity and Typicality

The Likelihood Ratio Framework

The LR provides a coherent framework for updating beliefs about competing hypotheses in light of new evidence. It is formally expressed as:

In FTC, typical hypotheses are:

• Hp: The suspect is the author of the questioned document.
• Hd: Some other person, not the suspect, is the author of the questioned document [6].

The prior odds (the fact-finder's belief before considering the linguistic evidence) is updated by the LR to yield the posterior odds, as per the odds form of Bayes' Theorem [6]. The forensic linguist's role is to calculate the LR; they are not in a position to know, and should not present, the posterior odds [6].

Operationalizing Similarity and Typicality

• P(E|Hp) (Similarity): This component assesses how well the linguistic features of the questioned document align with the writing style of the suspect. A high probability indicates a high degree of similarity between the suspect's known writings and the questioned text.
• P(E|Hd) (Typicality): This component assesses how distinctive the observed similarity is. It evaluates how common or rare the linguistic features are in a broader, relevant population of writers. A low probability indicates that the features are unusual, thus strengthening the evidence if similarity is high [6].

The ultimate strength of the evidence depends on the combination of both components. Strong evidence is characterized by high similarity and low typicality (i.e., the features are consistent with the suspect but rare in the general population).

Experimental Protocols for LR-Based FTC

Core Protocol: System Validation with Topic Mismatch

Validation is a critical step to ensure that an FTC system provides scientifically defensible and reliable LRs. It has been argued that validation must replicate the conditions of the case under investigation using relevant data [2] [6]. The following protocol uses a mismatch in topics between known and questioned texts as a case study.

1. Objective: To empirically validate an FTC system's performance under forensically realistic conditions where the topic of the questioned document differs from the topics in the suspect's known writings.

2. Materials and Reagents:

• Text Corpora: A collection of texts from a large number of authors (e.g., 115 authors or more) [7].
• Software: Computational environment for text processing and statistical modeling (e.g., R, Python).
• Feature Extraction Tools: Scripts to extract linguistic features from raw text.

3. Procedure:

• Step 1: Define Conditions. Create two experimental sets:
  • Set A (Validation-focused): Designs validation experiments to reflect casework conditions. For a topic mismatch study, this involves ensuring that the known and questioned texts for a given author are on different topics [2] [6].
  • Set B (Non-validation-focused): Does not control for topic mismatch, potentially using texts on the same topic for known and questioned documents [2] [6].
• Step 2: Feature Extraction. For each set of documents (known and questioned), extract quantitative linguistic features. Common features include [7]:
  • N-grams: Sequences of n characters or words.
  • Stylometric Features: Vocabulary richness, average sentence length, ratio of function words, etc.
• Step 3: Calculate Likelihood Ratios. Compute LRs using a statistical model. The Dirichlet-multinomial model is one suitable approach, followed by logistic regression calibration [2] [6].
• Step 4: Assess System Performance. Evaluate the quality of the derived LRs using:
  • Log-Likelihood-Ratio Cost (Cllr): A single metric that measures the average cost of the LRs, with lower values indicating better performance [7]. Cllr can be decomposed into Cllr_min (reflecting discriminability) and Cllr_cal (reflecting calibration loss) [7].
  • Tippett Plots: Visualizations that show the cumulative proportion of LRs for both same-author and different-author comparisons, allowing for an assessment of the strength and validity of the evidence across many tests [2] [7].
• Step 5: Compare Results. Compare the Cllr values and Tippett plots from Set A and Set B. The experiment demonstrates that Set B, which overlooks casework conditions, may yield overly optimistic or misleading performance, thus highlighting the necessity of proper validation [2] [6].

Protocol: Logistic Regression Fusion for Evidence Strength

To improve the robustness and performance of an FTC system, LRs from multiple, different procedures can be combined.

1. Objective: To fuse LRs estimated from different feature sets (e.g., multivariate features, token N-grams, character N-grams) into a single, more accurate and informative LR.

2. Procedure:

• Step 1: Generate Multiple LR Sets. Calculate LRs for the same set of comparisons using at least three different procedures (e.g., MVKD with stylometric features, token N-grams, character N-grams) [7].
• Step 2: Apply Logistic Regression Fusion. Use logistic regression to combine the LRs from the different procedures into a single, fused LR for each author comparison. This technique is robust and has been successfully applied in various forensic comparison systems [7].
• Step 3: Validate Performance. Assess the performance of the fused system using Cllr and Tippett plots. The fused system has been demonstrated to outperform any of the single-procedure systems, particularly when the sample size of text is limited (e.g., 500-1500 tokens) [7].

Key Research Reagent Solutions

Table 1: Essential Materials and Tools for FTC Research

Item	Function in FTC Research
Chatlog/Email Corpus	A database of authentic (e.g., predatory chatlogs) or simulated texts from multiple authors, used for developing and validating FTC systems [7].
Feature Extraction Algorithms	Scripts (e.g., in Python/R) to convert raw text into quantitative features like N-grams and stylometric measurements, forming the basis for statistical modeling [7].
Statistical Modeling Environment (e.g., R)	A software platform for implementing complex statistical procedures, including Dirichlet-multinomial models, logistic regression calibration, and fusion [2] [7].
Validation Software/Code	Custom code or applications used to perform bootstrap validation and generate performance metrics like Cllr and calibration plots [8].

Data Presentation and Analysis

Quantitative Performance of FTC Systems

The following table summarizes hypothetical performance data (Cllr) for different system configurations, illustrating the impact of feature fusion and sample size, based on findings from the literature [7].

Table 2: Example Performance Metrics (Cllr) for Different FTC System Configurations Across Various Sample Sizes. Lower Cllr values indicate better performance.

System Configuration	500 Tokens	1000 Tokens	1500 Tokens	2500 Tokens
MVKD Procedure	0.45	0.31	0.24	0.19
Token N-grams Procedure	0.52	0.41	0.35	0.29
Character N-grams Procedure	0.49	0.38	0.31	0.25
Fused System	0.35	0.22	0.15	0.12

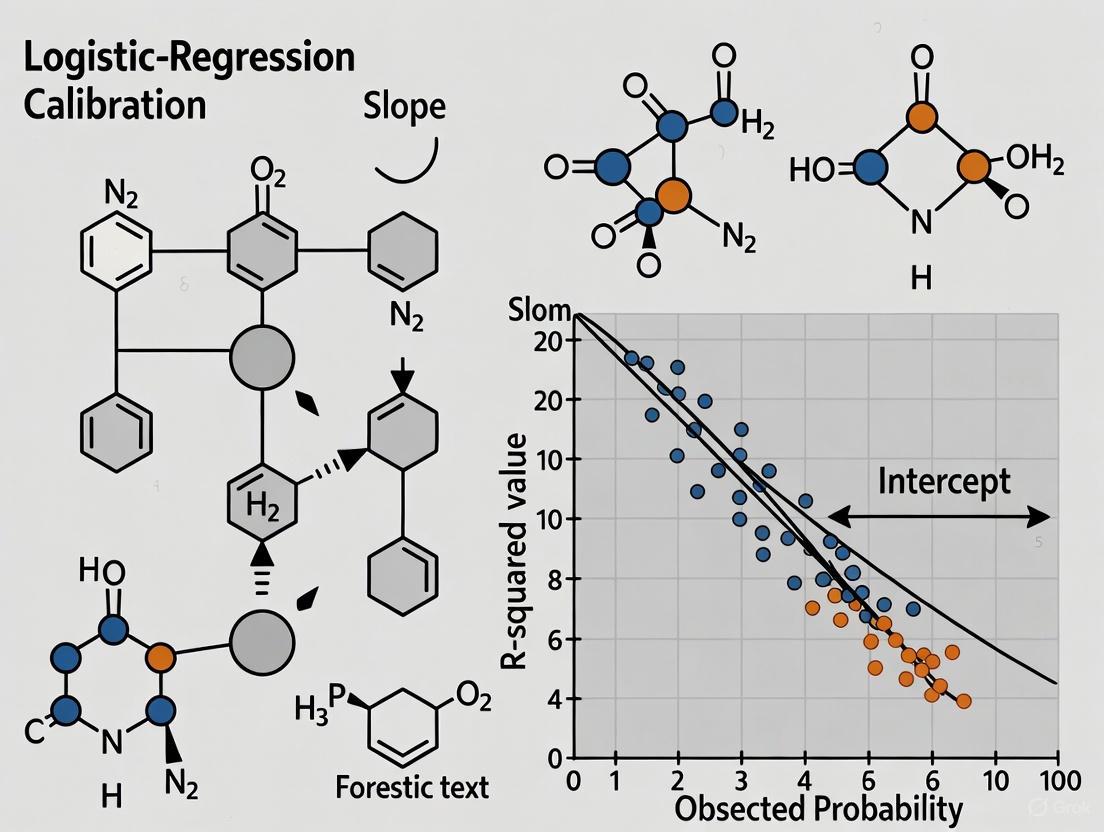
Calibration Assessment Metrics

Calibration refers to the agreement between estimated probabilities and observed outcomes. In clinical prediction models, it is vastly underreported but essential [9] [10]. The following table outlines key calibration metrics and their interpretation, which are directly applicable to assessing calibrated LRs in FTC.

Table 3: Metrics for Assessing the Calibration of a Predictive System

Calibration Metric	Description	Target Value	Interpretation of Deviation
Calibration-in-the-large (Intercept)	Compares the average predicted risk to the overall event rate [10].	0	Negative value: overestimation; Positive value: underestimation.
Calibration Slope	Evaluates the spread of the estimated risks [10].	1	Slope < 1: predictions are too extreme; Slope > 1: predictions are too modest.
Flexible Calibration Curve	A graphical plot (non-linear) of predicted vs. observed event probabilities [10].	Diagonal line	Curves below diagonal: overestimation; Curves above: underestimation.

Workflow and Pathway Visualizations

Forensic linguistics applies linguistic knowledge to legal and forensic contexts, often to determine the most likely author of a text in question. Traditional approaches have historically relied on expert subjective judgement, which can be susceptible to contextual biases and is difficult to validate objectively. This document outlines Application Notes and Protocols for implementing transparent, reproducible, and empirically validated methods, specifically through the framework of logistic-regression calibration for forensic text comparison. This shift towards a quantitative evidence evaluation framework is critical for improving the scientific rigor and admissibility of forensic text evidence in judicial processes.

Quantitative Comparison of Likelihood Ratio Estimation Methods

The core of a modern forensic text comparison involves calculating a Likelihood Ratio (LR), which quantifies the strength of the evidence under two competing propositions (e.g., the suspect is vs. is not the author of the questioned text) [11]. The following data, synthesized from empirical research, compares different methodological approaches for LR estimation.

Table 1: Empirical Comparison of Score-Based vs. Feature-Based LR Methods [12]

Method Category	Specific Model/Function	Key Feature	Performance (Cllr)	Best Use Case
Score-Based	Cosine Distance	Treats entire text as a single vector; uses similarity score.	~0.34 (Baseline)	Lower complexity analyses; initial exploratory work.
Feature-Based	One-Level Poisson Model	Models word counts; accounts for over-dispersion.	0.14-0.20 improvement over baseline	General text evidence with common words.
	One-Level Zero-Inflated Poisson Model	Accounts for frequent absence of many words in a text.	0.14-0.20 improvement over baseline	Texts with a high number of rare or absent words.
	Two-Level Poisson-Gamma Model	Hierarchical model; captures variability between and within authors.	0.14-0.20 improvement over baseline (Best overall)	Complex data; offers robust performance for formal casework.

Table 2: Interpretation of Likelihood Ratio (LR) Values [11]

LR Value Range	Verbal Equivalent (Support for H1 over H2)
1 < LR ≤ 10	Weak Support
10 < LR ≤ 10²	Moderate Support
10² < LR ≤ 10³	Moderately Strong Support
10³ < LR ≤ 10⁴	Strong Support
10⁴ < LR ≤ 10⁵	Very Strong Support
LR > 10⁵	Extremely Strong Support

Experimental Protocols for Forensic Text Comparison

Protocol 1: Corpus Preparation and Feature Extraction

Objective: To construct a representative reference corpus and extract a standardized set of linguistic features for analysis.

• Data Collection:

  • Gather a large collection of known-author texts (e.g., from 2,157 authors, as in the cited study) [12].
  • Ensure metadata (author, date, genre) is meticulously documented.
  • Open Science Practice: Store all raw data in an open-access repository with a clear license to facilitate verification and replication [13].

• Text Pre-processing:

  • Convert all text to lowercase to ensure case-insensitive analysis.
  • Remove punctuation, numbers, and other non-lexical characters.
  • (Optional) Apply lemmatization or stemming to group different forms of the same word.

• Feature Selection - Bag-of-Words Model:

  • Create a document-term matrix that counts the occurrence of each word in each document.
  • Select the n-most frequently occurring words across the entire corpus (e.g., the 400 most common words) [12]. These common words, often function words (e.g., "the," "and," "of"), are highly subconscious and thus stylistically revealing.

Protocol 2: Feature-Based LR Estimation using Poisson Models

Objective: To implement a feature-based likelihood ratio estimation system using a Two-Level Poisson-Gamma model.

• Model Training:

  • For each of the k selected features (e.g., 400 common words), fit a Poisson-based model to characterize an author's writing style.
  • The Two-Level Poisson-Gamma model is hierarchical:
    • Level 1 (Within-Author): Models the word counts for a given author as following a Poisson distribution.
    • Level 2 (Between-Author): Models the variability of Poisson parameters across different authors using a Gamma distribution.
  • Use the trained model to estimate the probability of observing the feature counts in the questioned text, given the author is a specific individual versus given the author is from a relevant population.

• Logistic Regression Fusion and Calibration:

  • The outputs (log-likelihoods) from the multiple Poisson models are used as input features for a logistic regression model [12] [11].
  • This logistic regression model is trained to fuse the evidence from all features and output a well-calibrated Likelihood Ratio.
  • Calibration is critical: It ensures that an LR of 100 truly represents 100 times more likely, not just a high score. Performance is evaluated using the log-likelihood ratio cost (Cllr), which separately assesses discrimination (Cllrmin) and calibration (Cllrcal) [12].

Protocol 3: Validation and Performance Evaluation

Objective: To rigorously validate the developed model and ensure its performance meets standards for forensic application.

• Experimental Design:

  • Use a balanced set of same-author and different-author text comparisons.
  • Employ a k-fold cross-validation approach to ensure results are generalizable and not over-fitted to the training data.

• Performance Metrics:

  • Calculate the Cllr as the primary metric. A lower Cllr indicates a better-performing system [12].
  • Analyze the Tippett plot to visualize the distribution of LRs for same-author and different-author cases.
  • Report the Cllrmin (potential discrimination) and Cllrcal (calibration cost) to diagnose system performance [12].

Workflow Visualization: Transparent Forensic Text Comparison

The following diagram outlines the complete, reproducible workflow for a forensic text comparison, from data acquisition to reporting.

The Scientist's Toolkit: Essential Research Reagents and Solutions

Table 3: Key Reagents and Computational Tools for Reproducible Forensic Linguistics

Item Name	Type/Function	Application in Protocol	Notes for Reproducibility
Reference Text Corpus	Data	Protocol 1	A large, relevant collection of known-author texts. Must be shared publicly or described with sufficient metadata [13].
Bag-of-Words Feature Set	Data	Protocol 1, 2	The specific list of n-most frequent words used. The value of n and the final word list must be documented.
Poisson-Gamma Model	Computational Algorithm	Protocol 2	The core statistical model for capturing authorial style. Code implementation must be shared [12].
Logistic Regression Calibrator	Computational Algorithm	Protocol 2	Fuses feature outputs into a calibrated LR. Prevents "overstatement" of evidence [11].
Cllr (and Cllrmin/Cllrcal)	Validation Metric	Protocol 3	The standard for evaluating system performance. Must be reported for any developed system [12].
R/Python Scripts	Software	All Protocols	Code for the entire workflow, from pre-processing to validation, must be open-source and version-controlled [13].
CAY10746	CAY10746, MF:C26H23N3O5, MW:457.5 g/mol	Chemical Reagent	Bench Chemicals
Elsinochrome A	Elsinochrome A, MF:C30H24O10, MW:544.5 g/mol	Chemical Reagent	Bench Chemicals

Forensic Text Comparison (FTC) involves the scientific analysis of textual evidence to address questions of authorship. A scientifically defensible approach requires a paradigm shift from subjective linguistic analysis to methods based on quantitative measurements, statistical models, and the likelihood-ratio (LR) framework, all empirically validated under casework conditions [6]. This application note details protocols for implementing such a methodology, with a specific focus on the use of logistic-regression calibration to compute LRs in the presence of complex influences from idiolect, topic, and genre. We demonstrate that rigorous validation using relevant data replicating case conditions is critical to avoid misleading the trier-of-fact [6].

The evaluation of forensic evidence comprises two core processes: analysis, the extraction of information from items of interest, and interpretation, drawing inferences about the meaning of the extracted information [14]. In FTC, traditional methods relying on human perception and subjective judgment are increasingly being replaced by a new paradigm known as Forensic Data Science. This paradigm is characterized by four key elements [6] [14]:

• The use of quantitative measurements from textual data.
• The use of statistical models for data interpretation.
• The use of the likelihood-ratio (LR) framework for evaluating the strength of evidence.
• Empirical validation of methods and systems under realistic casework conditions. This paradigm shift produces methods that are transparent, reproducible, and intrinsically resistant to cognitive bias [6]. The following sections provide detailed protocols for applying this paradigm, particularly using logistic regression, to the complex problem of textual evidence.

Core Concepts and the Likelihood-Ratio Framework

The Nature of Textual Evidence

A text is a complex datum encoding multiple layers of information, which must be disentangled in FTC [6]:

• Idiolect: An individuating way of speaking and writing, which is the target of authorship analysis [6].
• Group-Level Information: Includes author demographics (e.g., gender, age, socioeconomic background) [6].
• Communicative Situation: Encompasses genre, topic, formality, the author's emotional state, and the intended recipient, all of which can influence writing style [6].

The Likelihood Ratio Explained

The LR is a logical framework for evaluating the strength of evidence under two competing propositions [6] [15]. In the context of FTC, these are typically:

• Hp: The prosecution hypothesis (e.g., the suspect is the author of the questioned document).
• Hd: The defense hypothesis (e.g., someone other than the suspect is the author of the questioned document).

The LR is calculated as the ratio of two conditional probabilities: LR = p(E | Hp) / p(E | Hd) where E represents the quantified stylistic evidence extracted from the questioned and known documents [6] [15].

An LR > 1 supports Hp, while an LR < 1 supports Hd. The further the value is from 1, the stronger the evidence. The LR updates the prior beliefs of the trier-of-fact (judge or jury) via Bayes' Theorem [6]: Posterior Odds = Prior Odds × LR

Table 1: Interpretation of Likelihood Ratio Values

LR Value	Verbal Equivalent (Support for Hp)
> 10⁵	Extremely Strong
10⁴ to 10⁵	Very Strong
10³ to 10⁴	Strong
10² to 10³	Moderately Strong
10¹ to 10²	Moderate
1 to 10¹	Weak
1	Inconclusive
Reciprocal values	Equivalent support for Hd

Experimental Protocols for Forensic Text Comparison

Core Experimental Workflow

The following diagram illustrates the end-to-end workflow for a validated FTC study, from data collection to reporting.

Protocol 1: Data Collection and Curation for Validation

Objective: To construct a validation dataset that meets the two critical requirements of reflecting case conditions and being relevant to the case [6].

Procedure:

• Define Case Conditions: Identify the specific conditions of the case under investigation. As a case study, we focus on topic mismatch between known and questioned documents, a known challenging factor in authorship analysis [6].
• Source Relevant Data: Collect textual data from relevant populations and covering the topics of interest. For a case with topic mismatch, this requires:
  • A set of known documents (K) from a candidate author on one or more specific topics.
  • A questioned document (Q) on a different topic.
  • A reference set of documents from a relevant population of potential authors, which includes texts on the same topic as Q and the same topic as K.
• Simulate Mismatch Conditions: For validation experiments, create two conditions:
  • Matched-Topic Condition: Compare Q and K documents on the same topic.
  • Mismatched-Topic Condition: Compare Q and K documents on different topics.
• Data Partitioning: Split the data into training sets (for model development) and test sets (for validation) to ensure unbiased performance evaluation.

Protocol 2: Feature Extraction and LR Calculation with a Dirichlet-Multinomial Model

Objective: To extract quantitative features from texts and compute uncalibrated likelihood ratios.

Procedure:

• Text Pre-processing:
  • Clean the text (remove headers, footers, metadata).
  • Apply tokenization, lowercasing, and lemmatization as required.
• Feature Selection: Extract a set of linguistic features. Common features in FTC include:
  • Lexical: Character n-grams, word n-grams, function words, vocabulary richness.
  • Syntactic: Punctuation marks, sentence length, part-of-speech tags.
  • Structural: Paragraph length, text layout features.
• Model Training (Dirichlet-Multinomial):
  • This model is a popular choice for text classification and authorship attribution as it accounts for the "burstiness" of words (the tendency for a word to appear repeatedly in a document).
  • Train the model on the feature counts from the known documents of the candidate author and the reference corpus.
• Calculate Uncalibrated LR: The model outputs a score representing the probability of the evidence (the features in Q) given the author of K versus given an author from the reference population. This score is used as the uncalibrated LR.

Protocol 3: Logistic Regression Calibration

Objective: To transform the output of a statistical model (the uncalibrated LR) into a well-calibrated likelihood ratio, ensuring its validity as a measure of evidence strength [6] [14].

Rationale: Raw scores from models like the Dirichlet-multinomial are often not well-calibrated. Logistic regression is a powerful and widely used method for calibrating these scores, particularly in forensic voice comparison and other disciplines [15].

Procedure:

• Generate Scores for Calibration Set: Using a separate calibration dataset (not the test set), compute a set of uncalibrated LRs for many pairs of same-author and different-author comparisons.
• Fit Logistic Regression Model: The logistic regression model is trained to predict the binary outcome (same-author vs. different-author) from the log of the uncalibrated LR.
  • Independent Variable: The log of the uncalibrated LR (log(LR_raw)).
  • Dependent Variable: The class label (e.g., 1 for same-author, 0 for different-author).
• Apply Calibration: The fitted logistic regression model maps the input log(LR_raw) to a calibrated probability, which can then be transformed into the final, calibrated LR.
• Advanced Calibration (Bi-Gaussian): For higher performance, a bi-Gaussian calibration method can be employed. This method maps the empirical scores to a "perfectly-calibrated bi-Gaussian system" where the log(LR) distributions for same-source and different-source inputs are Gaussian with equal variance and means of +σ²/2 and -σ²/2, respectively [14].

Table 2: Key Research Reagent Solutions for FTC

Reagent / Tool	Function / Explanation
Reference Corpus	A collection of texts from a relevant population of potential authors. It is essential for estimating the background typicality of features under Hd [6].
Dirichlet-Multinomial Model	A statistical model used for text classification that handles the discrete, multivariate nature of text data and accounts for word "burstiness." Used for initial LR calculation [6].
Logistic Regression Calibration	A statistical method that maps raw model scores to well-calibrated LRs, ensuring the output accurately represents the strength of evidence [6] [15].
Log-Likelihood-Ratio Cost (Cllr)	A single scalar metric for evaluating the performance of an LR system, incorporating both discrimination and calibration. Lower values indicate better performance [6] [14].
Tippett Plot	A graphical tool for visualizing the distribution of LRs for both same-source and different-source comparisons, allowing for easy assessment of system validity and error rates [6].

Validation and Performance Metrics

Objective: To empirically validate the performance and reliability of the FTC system under conditions reflecting casework.

Procedure:

• Calculate Log-Likelihood-Ratio Cost (Cllr):
  • Cllr is the primary metric for evaluating an LR system's overall performance. It is calculated using the following formula on a separate test set: Cllr = (1/2) * [ Σ logâ‚‚(1 + 1/LRi) for same-author pairs + Σ logâ‚‚(1 + LRj) for different-author pairs ] / N
  • A lower Cllr indicates a better system. A perfectly calibrated and discriminating system would have a Cllr of 0.
• Generate Tippett Plots:
  • These plots display the cumulative distributions of the log(LR) values for both same-author and different-author comparisons.
  • They visually demonstrate the separation between the two distributions and allow for the assessment of observed error rates at any decision threshold.

The diagram below illustrates the logical relationship between the system output, calibration, and the final validated LR.

Critical Discussion and Future Research

The application of the forensic data science paradigm to textual evidence reveals several unique challenges and future research directions [6]:

• Defining Casework Conditions: Further research is needed to determine the full range of casework conditions (beyond topic mismatch, e.g., genre, register, time interval) and mismatch types that require specific validation.
• Relevant Data: There is a need for clear guidelines on what constitutes "relevant data" for a case, including the definition of appropriate reference populations and the sufficiency of data from a candidate author.
• Data Requirements: Research must establish the minimum quality and quantity of textual data required for both known documents and reference corpora to achieve reliable and valid results.

Empirical validation is a cornerstone of robust scientific research, ensuring that findings are not merely products of chance or specific experimental contingencies. Within the specialized field of forensic text comparison, where logistic regression models are increasingly used for calibration, the principles of validation carry immense weight. The core requirements for such validation are twofold: the ability to replicate case conditions and the imperative to use relevant data. These requirements ensure that the performance of a method or model, once validated, is trustworthy and applicable to real-world casework. This article details the application notes and protocols for meeting these core requirements, providing a framework for researchers and practitioners in forensic science and related disciplines.

Foundational Concepts: Reproducibility vs. Replicability

A clear understanding of the distinction between reproducibility and replicability is fundamental to designing a sound validation study. In the context of simulation studies and empirical research, these terms have specific, distinct meanings [16].

• Reproducibility is defined as generating the exact same results using the exact same data and the exact same analysis. It is considered a minimum standard for scientific research. In computational fields, this can extend to using the same data-generating process, even if the exact raw data cannot be recovered (e.g., if a random seed was not set) [16].
• Replicability involves producing similar results using different data and performing the same analysis. For empirical research, this means collecting new data following the original procedures as closely as possible. For simulation studies, it entails writing new code to generate and analyze data based on the procedural descriptions in the original publication [16].

The following table summarizes these key concepts:

Table 1: Definitions of Reproducibility and Replicability

Concept	Definition	Implementation in Simulation Studies	Purpose
Reproducibility	Producing the same results using the same data and analysis.	Applying original analysis scripts to original data or data newly generated with the original script.	A minimum standard to verify no errors in the original analysis.
Replicability	Producing similar results using different data and the same analysis.	Writing new code to generate and analyze data, following the original study's procedures.	Provides additional evidential weight and tests the generalizability of findings.

For forensic text comparison, the ultimate goal of empirical validation is often replicability—demonstrating that a calibrated logistic regression model performs reliably not just on the data it was built on, but on new, independent data that represents the varying conditions of actual casework.

The Critical Role of Replication in Validation

Replication is not merely a technical exercise; it is a crucial mechanism for building a robust and reliable evidence base. Its importance is multi-faceted [17] [18]:

• Guard Against Pseudoscience: Replication acts as a bulwark against pseudoscience by subjecting claims of efficacy to independent empirical testing. Practices that cannot withstand replication attempts are revealed as unreliable [17].
• Control for Biases and Errors: Independent replication, conducted by researchers not involved in the original study, minimizes the potential influence of researcher biases and unintentional errors that can skew results [17].
• Identify Effective Components: Through replication and extension studies, researchers can identify which components of a complex methodological package are universally effective and which are context-dependent [17].
• Build Scientific Knowledge: As a neutral process, replication advances scientific discovery and theory by introducing new evidence, regardless of whether it confirms the original findings. A failure to replicate can push research in new, creative directions [18].

In forensic science, where conclusions can have significant legal consequences, a failure to replicate a method's performance under case-like conditions should be a major red flag, indicating that the method is not yet sufficiently validated for casework application.

Core Requirement 1: Replicating Case Conditions

The first core requirement demands that validation studies replicate, as closely as possible, the conditions under which a method will be applied in real casework. This involves a detailed understanding and simulation of the sources of variability encountered in forensic practice.

Protocols for Replicating Case Conditions

• Define the "Case Condition" Universe: Identify and document all relevant parameters of a forensic text case. This includes:

  • Text Characteristics: Genre (e.g., text message, formal email, social media post), register, topic, and length.
  • Author Demographics: Potential variations in age, gender, dialect, socio-economic background, and education level.
  • Data Collection Circumstances: Device type, platform, and any environmental factors that may influence the text.
  • Case Preconditions: The specific propositions (e.g., same author vs. different author) and the relevant population of potential authors.

• Implement a Replicable Data Generation Process: For logistic regression calibration, this involves creating a structured framework for generating training and testing datasets.

  • Scripted Workflows: Use scripted code for all data generation and analysis steps to ensure transparency and reproducibility [16].
  • Seed Setting: Document and set random number generator seeds where applicable to ensure the data-splitting and sampling processes can be reproduced exactly [16].
  • Stratified Sampling: When drawing from a larger population of text samples, use stratified sampling to ensure that all defined case conditions are adequately represented in the validation dataset.

The workflow for designing a validation study that replicates case conditions can be summarized as follows:

Facilitators and Hindrances to Replicability

Research into the replicability of statistical simulation studies has identified key factors that help or hinder the process [16].

Table 2: Factors Affecting the Replicability of Studies

Facilitating Factors	Hindering Factors
Availability of original code and data	Lack of detailed information in the original publication
Detailed reporting or visualization of data-generating procedures	Unsubstantiated or vague methodological descriptions
Expertise of the replicator	Sustainability of information sources (e.g., broken links)

Core Requirement 2: Using Relevant Data

The second core requirement insists that the data used for validation must be relevant to the specific propositions and conditions of the case at hand. Using convenient but irrelevant data fundamentally undermines the validity of the conclusions.

The Concept of "Relevant Data"

In the context of forensic text comparison, "relevant data" refers to a well-specified set of text samples that is representative of the population of potential sources under the given case propositions. For example, validating a method intended to distinguish between authors of technical reports using a corpus of informal text messages is not a relevant validation.

Protocols for Sourcing and Using Relevant Data

• Data Use Oversight and Ontologies: For sensitive data, employ a formal data use oversight process. Automated systems like the Data Use Oversight System (DUOS) can use ontologies (e.g., GA4GH Data Use Ontology) to ensure that dataset access and usage are compatible with the intended validation purpose and legal-ethical constraints [19].
• Internal Validation with Large, Representative Datasets: When developing a prediction model, use internal validation methods that maximize the use of available relevant data to obtain accurate performance estimates.
  • Avoid Simple Data-Splitting: Especially with rare events (e.g., a specific writing style), splitting data into a single training and test set reduces statistical power for both model estimation and validation [20].
  • Prefer Cross-Validation: Use cross-validation (e.g., 5x5-fold cross-validation) on the entire dataset. This approach uses all relevant data for estimation while providing a robust estimate of model performance by repeatedly testing on out-of-fold data [20].
  • Cautious Use of Bootstrap Optimism Correction: While sometimes recommended, bootstrap optimism correction can overestimate model performance, particularly for complex models like random forests with rare-event outcomes. Cross-validation is often more reliable [20].

The following diagram illustrates the logic for selecting an appropriate internal validation method to ensure the use of relevant data:

Table 3: Comparison of Internal Validation Methods for Using Relevant Data

Validation Method	Description	Advantages	Disadvantages	Suitability for Rare Events
Split-Sample	Data divided into a single training set and a single testing set.	Simple to implement and explain.	Reduces statistical power; highly variable performance estimates with rare events.	Poor
Cross-Validation	Data divided into k folds; model trained on k-1 folds and validated on the held-out fold, repeated for all folds.	Maximizes data use for training; provides a robust performance estimate.	Computationally intensive; can be variable if not repeated.	Good
Bootstrap Optimism Correction	Multiple bootstrap samples are drawn with replacement; model is trained on each and tested on full sample to estimate optimism.	Efficient use of data.	Can overestimate performance for complex, machine-learning models with rare outcomes.	Fair (but requires verification)

The Scientist's Toolkit: Essential Reagents for Validation

The following table details key "research reagent solutions" or essential components required for conducting empirical validation in this field.

Table 4: Essential Research Reagents and Materials for Empirical Validation

Item	Function in Validation	Example/Notes
Curated Text Corpora	Serves as the foundational population data for model training and testing.	Must be relevant to case conditions (e.g., genre, dialect, time period). Annotated with known author metadata.
Data Use Ontology (DUO)	Ensures ethical and legally compliant use of data by formally encoding permissible use conditions.	Used by systems like DUOS to automatically manage dataset access [19].
Scripting Environment (e.g., R, Python)	Provides a reproducible and transparent platform for all data generation, analysis, and modeling tasks.	Scripts should be version-controlled and shared to facilitate replication [16].
Logistic Regression Software	The core engine for calibrating the model that outputs likelihood ratios (LRs).	Includes standard packages (e.g., glm in R) and penalized versions (e.g., logistf for Firth regression) to handle data separation [21].
Likelihood Ratio (LR) Calculation Framework	The statistical framework for expressing the strength of forensic evidence.	Moves beyond simple classification to provide a balanced ratio of probabilities under competing propositions [21].
Validation Metrics Suite	A set of tools to quantitatively assess model performance.	Includes measures of discrimination (AUC) and, critically, calibration metrics (e.g., calibration plots) to ensure LR values are not misleading [5].
Hortein	Hortein, MF:C20H12O6, MW:348.3 g/mol	Chemical Reagent
GDC-0134	GDC-0134, CAS:1637394-01-4, MF:C19H20F4N6O2, MW:440.4 g/mol	Chemical Reagent

The core requirements for empirical validation—replicating case conditions and using relevant data—are interdependent pillars of robust forensic science. Adhering to these principles, supported by the detailed protocols and tools outlined in this article, allows researchers to build and validate logistic regression models for forensic text comparison with greater confidence. Transparent reporting of all implementation details, public availability of code, and the use of rigorous internal validation methods are non-negotiable practices. By embracing these standards, the field can produce findings that are not only scientifically sound but also forensically relevant, reliable, and ultimately, fit for purpose in a justice system.

From Scores to Likelihood Ratios: A Step-by-Step Guide to Logistic-Regression Calibration

In forensic text comparison (FTC) and many other scientific disciplines, the strength of evidence is ideally expressed using a Likelihood Ratio (LR). The LR quantifies the support the evidence provides for one proposition relative to an alternative proposition [21] [7]. Directly outputted raw scores from machine learning models or statistical functions, however, are not interpretable as LRs. This application note, framed within a broader thesis on logistic-regression calibration for FTC research, elucidates this critical distinction and outlines the validated protocols necessary to transform uninterpretable raw scores into forensically sound LRs.

The core problem lies in the fact that raw scores are uncalibrated. They typically lack a meaningful scale, do not accurately represent the relative probabilities of the evidence under the two competing hypotheses, and can be highly sensitive to the specific dataset used, leading to potentially misleading over- or under-statement of evidential strength [22] [23]. Proper calibration, particularly using logistic regression, is therefore not an optional step but a fundamental requirement for a scientifically defensible LR system.

The Problem with Raw Scores: Key Limitations

Raw scores, often derived from measures of similarity or typicality, fail as LRs for several interconnected reasons.

• They are Unanchored and Lack a Meaningful Scale: A raw score's value is arbitrary. A score of 10 from one model or dataset is not equivalent to a score of 10 from another. In contrast, an LR has a fixed, probabilistic interpretation: an LR of 10 means the evidence is 10 times more likely under H1 than under H2 [21].
• They Ignore Typicality in the Relevant Population: Research has demonstrated that scores which are purely measures of similarity produce poor results. A forensically interpretable LR must account for both the similarity between the known-source and questioned-source items and the typicality of the questioned-source specimen with respect to the relevant population defined by the defence hypothesis (H2). A high similarity to a known source is weak evidence if the features are also highly typical of the general population [24].
• They are Often Misleading and Poorly Calibrated: Without calibration, raw scores can systematically misrepresent the strength of evidence. A score might consistently overstate the evidence (e.g., a score that should correspond to an LR of 10 is consistently outputted for evidence that only warrants an LR of 5) or understate it. The log-likelihood ratio cost (Cllr) is a key metric that penalizes such misleading LRs, especially those further from 1 [22].

Table 1: Core differences between raw scores and calibrated Likelihood Ratios.

Feature	Raw Scores	Calibrated Likelihood Ratios
Interpretation	Arbitrary, model-specific	Probabilistic, universal
Scale	Unbounded or poorly defined	0 to +∞, with LR=1 as neutral
Evidential Basis	Often similarity-only	Similarity & typicality
Calibration	Uncalibrated	Calibrated to reflect true strength
Forensic Validity	Low, potentially misleading	High, scientifically defensible

Quantitative Evidence: The Impact of Calibration

The necessity of calibration is empirically demonstrated by the improvement in system performance metrics, primarily the Cllr. The Cllr measures the overall performance of an LR system, with a lower value indicating a better system (0 is perfect, 1 is uninformative) [22]. It can be decomposed into Cllrmin (reflecting inherent discrimination power) and Cllrcal (reflecting calibration error).

In a study on linguistic text evidence, fusion of LRs from multiple procedures via logistic regression improved performance, particularly with small sample sizes. The results below show how Cllr values improve post-calibration and vary with data relevance [7] [23].

Table 2: Example Cllr values from forensic text comparison studies demonstrating the effect of calibration and data relevance.

Study Context	Condition / System	Cllr Value	Interpretation
Linguistic Text Evidence [7]	Fused System (Best Performance)	~0.2 (estimated from graph)	Good performance
Cross-Topic Text Comparison [23]	Cross-topic 1 (Matched to casework)	Highest (Worst)	Highlights need for relevant data
Cross-Topic Text Comparison [23]	Any-topics setting	Lower than mismatched topics	Using irrelevant data can be detrimental
General LR Systems [22]	Uninformative System	1.0	Baseline for poor performance
General LR Systems [22]	Good Performance	~0.3 (from review)	Example of a target value

Experimental Protocols

Protocol 1: The Two-Stage LR Calculation Pipeline

This is the standard workflow for producing calibrated LRs in forensic text comparison and other domains [7] [23].

1. Objective: To calculate a calibrated Likelihood Ratio from raw data. 2. Materials: * A set of known-source and questioned-source data. * Three mutually exclusive datasets: Training, Test, and Calibration sets. 3. Procedure: * Stage 1: Score Calculation * Using the Training set, develop a statistical model (e.g., Dirichlet-multinomial for text, penalized logistic regression for chemistry) [21] [23]. * For each pair of specimens in the Test and Calibration sets, input their feature data into the model to obtain a raw similarity or typicality score. * Stage 2: Calibration * Use the scores and ground truth labels (e.g., same-author/different-author) from the Calibration set to fit a calibration model, typically logistic regression [7] [23]. * This model learns the mapping from the uninterpretable raw scores to well-calibrated log-odds, which are then converted to LRs. 4. Analysis: The output of the calibration model is the final, forensically interpretable LR for each evidential pair.

Protocol 2: System Validation using Cllr

This protocol is critical for assessing the performance and reliability of the LR system [22].

1. Objective: To empirically validate the performance of an LR system using the log-likelihood ratio cost (Cllr). 2. Materials: * A set of empirical LRs generated by the system from Protocol 1 for a validation dataset. * The ground truth labels (H1-true or H2-true) for all samples in the validation set. 3. Procedure: * Calculate Cllr using the formula: Cllr = 1/2 * [ (1/N_H1) * Σ log₂(1 + 1/LR_i) + (1/N_H2) * Σ log₂(1 + LR_j) ] where LRi are LRs for H1-true samples and LRj are LRs for H2-true samples [22]. * Apply the Pool Adjacent Violators (PAV) algorithm to the LRs to calculate Cllrmin, which represents the best possible calibration for the system's inherent discrimination power. * Calculate the calibration error as Cllrcal = Cllr - Cllrmin. 4. Analysis: A low Cllr indicates good overall performance. A large Cllrcal suggests the LRs are poorly calibrated and require adjustment, even if the system's discrimination (Cllr_min) is good.

Conceptual Framework and Visualization

The following diagram illustrates the conceptual relationship between raw scores, calibration, and the properties of a forensically valid LR system.

The Scientist's Toolkit: Essential Research Reagents

Table 3: Key materials and methodological solutions for building and validating an LR system.

Category / 'Reagent'	Function / Explanation	Example Applications
Statistical Models (Score Generation)
Dirichlet-Multinomial Model	Calculates raw scores based on multivariate count data (e.g., word frequencies).	Forensic text comparison [23]
Penalized Logistic Regression	Generates scores while handling data separation and high-dimensionality.	Forensic toxicology (biomarker classification) [21]
Multivariate Kernel Density (MVKD)	Models feature vectors to calculate a score based on probability densities.	Forensic voice & text comparison [7]
Calibration Methods
Logistic Regression Calibration	The primary method for mapping raw scores to calibrated log-LRs.	Standard practice in forensic voice, text, and biometrics [7] [23]
Pool Adjacent Violators (PAV)	A non-parametric algorithm used to assess discrimination power (Cllr_min).	Validation and decomposition of Cllr [22]
Validation & Performance Metrics
Log-Likelihood Ratio Cost (Cllr)	A scalar metric that measures the overall quality of a set of LRs.	System validation across forensic disciplines [22] [7]
Tippett Plots	A graphical display showing the cumulative distribution of LRs for H1-true and H2-true cases.	Visual assessment of system performance [7]
Empirical Cross-Entropy (ECE) Plots	A plot that generalizes Cllr to unequal prior probabilities.	Robust performance assessment [22]
dCBP-1	dCBP-1, MF:C51H63F2N11O10, MW:1028.1 g/mol	Chemical Reagent
RIG012	RIG012, MF:C23H21NO3, MW:359.4 g/mol	Chemical Reagent

In forensic text comparison, the task of quantifying the strength of evidence is paramount. The likelihood ratio (LR) framework provides a logically valid and coherent structure for this purpose, allowing experts to evaluate evidence under two competing propositions [15]. Logistic regression calibration serves as a powerful methodological bridge, converting raw, uncalibrated similarity scores from a forensic-comparison system into interpretable likelihood ratios. This process is fundamentally an affine transformation, a concept central to the model defined by LR = A*score + B [25]. This document details the application notes and experimental protocols for implementing this affine transformation model within forensic text comparison research, providing scientists with a structured framework for robust evidence evaluation.

Theoretical Foundation: From Scores to Likelihood Ratios

The Likelihood Ratio Framework

The likelihood ratio is the cornerstone of interpretive forensic science. It is defined as the ratio of the probability of observing the evidence (E) under the prosecution's proposition (H1) to the probability of the evidence under the defense's proposition (H2) [15]: LR = P(E|H1) / P(E|H2)

The resulting LR value, which can range from 0 to +∞, expresses the strength of the evidence for one proposition over the other. A value of 1 indicates the evidence is inconclusive, while values greater than 1 support H1 and values less than 1 support H2 [15].

The Role of Logistic Regression Calibration

Raw scores generated by forensic comparison systems (e.g., measuring the similarity between two text samples) are often not directly interpretable as likelihood ratios. Their scale and distribution may not reflect true probabilities. Logistic regression calibration is a procedure for converting these scores to log likelihood ratios [25]. The core insight is that this conversion can be effectively achieved through an affine transformation—a linear transformation plus a constant—of the raw scores.

The affine transformation model for calibration is expressed as: log(LR) = A * score + B

Here, the raw score is transformed into a log-likelihood ratio by applying a slope (A) and an intercept (B). The likelihood ratio itself is then obtained by exponentiating the result: LR = exp(A * score + B). This simple model is also known as Platt scaling in the broader machine learning community [26] [27]. Its application ensures that the output is not only calibrated but also optimally informative for decision-making within the forensic context.

Experimental Protocols

Implementing the affine calibration model requires a rigorous, step-by-step experimental procedure. The following protocol ensures the reliability and validity of the calibrated likelihood ratios.

Stage 1: Data Preparation and Training

Objective: To prepare a dataset of known-origin and different-origin sample pairs for model training. Procedure:

• Sample Collection: Assemble a representative collection of text samples relevant to the forensic context (e.g., SMS messages, social media posts, documents).
• Pair Generation: For each sample, create comparison pairs.
  • Same-origin (SO) Pairs: Pairs known to originate from the same source (supporting H1).
  • Different-origin (DO) Pairs: Pairs known to originate from different sources (supporting H2).
• Feature Extraction & Scoring: Process each pair through a feature extraction algorithm (e.g., measuring n-gram frequencies, syntactic patterns, lexical richness) to generate a single, raw similarity score for each pair. The specific features are domain-dependent.
• Label Assignment: Assign binary labels to each score: 1 for SO pairs and 0 for DO pairs.
• Data Partitioning: Split the scored dataset into a training set and a test set. The training set is used to fit the calibration model, while the test set is reserved for its unbiased evaluation.

Stage 2: Model Fitting via Logistic Regression

Objective: To fit the affine calibration model (log(LR) = A * score + B) to the training data. Procedure:

• Model Specification: Use a logistic regression model with the raw similarity score as the sole predictor variable and the binary source label as the response variable.
• Parameter Estimation: Fit the model to the training data. The fitting process involves finding the parameters A (the coefficient of the score) and B (the intercept) that maximize the likelihood of the observed data [28].
• Parameter Output: Upon convergence, the model provides the estimates for A and B. These parameters define the affine transformation for calibration.

Stage 3: Calibration and Validation

Objective: To apply the fitted model to transform scores and to validate its performance on unseen data. Procedure:

• Transformation: For any new raw score (S) from a questioned sample pair, apply the calibrated model: Log-LR = A * S + B.
• Conversion: The likelihood ratio is computed as LR = exp(Log-LR).
• Validation: Use the held-out test set to evaluate the performance of the calibration.
  • Calibration Curve: Plot the predicted probability (from the logistic function) against the observed frequency of same-origin pairs in bins of predicted probability [26]. A well-calibrated model will align closely with the diagonal.
  • Discrimination Assessment: Evaluate the model's ability to distinguish between SO and DO pairs using metrics like the Area Under the ROC Curve (AUC).
• Fairness and Bias Check: It is critical to test for algorithmic bias by assessing calibration across different demographic subgroups (e.g., dialect, age group) to ensure the model does not perpetuate societal biases [27].

The entire experimental workflow, from data preparation to validation, is summarized in the diagram below.

The Scientist's Toolkit: Research Reagent Solutions

The following table details the essential components required for implementing the logistic regression calibration protocol.

Table 1: Essential Research Reagents and Materials for Logistic Regression Calibration

Item Name	Function / Description	Critical Notes for Practitioners
Reference Text Corpus	A collection of known-origin text samples used to generate same-origin and different-origin pairs for model training and testing.	Must be representative of the relevant population and casework to ensure ecological validity and avoid biased models [27].
Feature Extraction Algorithm	The computational method that converts a pair of text samples into a quantitative similarity score.	The choice of algorithm (e.g., based on stylometry, n-grams) is the primary determinant of the system's discriminative power.
Logistic Regression Software	A statistical computing environment (e.g., R, Python with scikit-learn) used to fit the calibration model and estimate parameters A and B.	Software like scikit-learn offers built-in functions for Platt scaling (CalibratedClassifierCV) [26].
Validation Dataset	A held-out set of scored sample pairs not used during model training, reserved for evaluating calibration performance.	Crucial for obtaining an unbiased assessment of the model's real-world performance and ensuring it has not overfitted the training data.
Performance Metrics	Quantitative measures such as the Brier Score, Log-Loss, and AUC used to assess calibration accuracy and discrimination [26] [27].	A lower Brier score indicates better calibration. AUC evaluates how well the scores separate SO and DO populations.
(Rac)-RK-682	(Rac)-RK-682, MF:C21H36O5, MW:368.5 g/mol	Chemical Reagent
Gallic acid-d2	Gallic acid-d2, MF:C7H6O5, MW:172.13 g/mol	Chemical Reagent

Data Analysis and Performance Metrics

The performance of the calibrated model must be rigorously quantified using standardized metrics. The following table outlines the key metrics and their interpretation.

Table 2: Key Performance Metrics for Evaluating Calibration Models

Metric	Formula / Principle	Interpretation in Forensic Context
Brier Score (BS)	BS = 1/N * ∑(y_i - p_i)^2 where y_i is the true label (0/1) and p_i is the predicted probability.	Measures the overall accuracy of probability assignments. A lower score (closer to 0) indicates better calibration. It is a proper scoring rule [26].
Log-Loss	Log Loss = -1/N * ∑[y_i * log(p_i) + (1-y_i)*log(1-p_i)]	A measure of the uncertainty of the probabilities based on the true labels. Lower values are better, with a perfect model having a log-loss of 0.
Calibration Curve	A plot of the predicted probabilities (binned) against the observed fraction of positive (SO) cases in each bin [26].	A well-calibrated model's curve will closely follow the diagonal line. Deviations indicate over-confidence (curve below diagonal) or under-confidence (curve above diagonal).
Area Under the ROC Curve (AUC)	Plots the True Positive Rate against the False Positive Rate at various classification thresholds.	Quantifies the model's power to discriminate between SO and DO pairs, independent of calibration. An AUC of 1 represents perfect discrimination, 0.5 represents chance.
Expected Calibration Error (ECE)	A weighted average of the absolute difference between the accuracy and confidence in each probability bin [27].	Provides a single-number summary of miscalibration. A lower ECE indicates a better-calibrated model.

The Affine Transformation in the Broader Calibration Context

The affine transformation is a specific instance of a calibrator. Its relationship to other calibration methods and the overall forensic process can be visualized as a decision flow. The simplicity of the LR = A*score + B model makes it robust, especially with limited data, but more flexible models like isotonic regression may be considered with larger datasets [26] [27].

The following diagram illustrates the logical pathway from a raw comparison score to a forensically interpretable likelihood ratio, highlighting the central role of the affine transformation.

In forensic text comparison research, the need for well-calibrated probabilistic outputs from classification models is paramount. The ability to report findings as meaningful Likelihood Ratios (LRs) is a fundamental requirement, as the LR provides a clear and balanced measure of the strength of evidence for one proposition against another [21]. Many powerful classifiers, including logistic regression, can produce uncalibrated probabilities, meaning their raw output scores do not faithfully represent true empirical likelihoods [26] [29]. Consequently, a deliberate calibration step is often necessary to ensure that a model's predicted probabilities are valid and interpretable.

A critical decision in this calibration process is the selection of data used to train the calibrator. Using the same data for both model fitting and calibration leads to overconfident predictions (biased towards 0 and 1) because the calibrator learns from data the model has already seen [26] [30]. This article details two robust methodologies to avoid this bias: using a separate, held-out dataset and employing cross-validation.

Core concepts and key terminology

• Probability Calibration: The process of adjusting the output probabilities of a classifier so that they reflect the true underlying probabilities of the outcomes. A model is well-calibrated if, for instance, among all samples for which it predicts a probability of 0.7, approximately 70% actually belong to the positive class [26].
• Calibrator: A regression model (e.g., logistic regression or isotonic regression) that maps the uncalibrated output scores of a classifier to calibrated probabilities on a scale of 0 to 1 [26].
• Likelihood Ratio (LR): In the context of forensic science, the LR is a ratio of the probability of observing the evidence under two competing propositions (e.g., prosecution and defense hypotheses). It is the fundamental metric for expressing the probative value of forensic evidence, including text comparisons [21].
• Data Leakage: A subtle but critical error where information from the test set, or data that should be independent, is used during the model training process. This leads to overly optimistic performance estimates and poor generalization on truly unseen data [31].

Table 1: Common Calibration Methods

Method	Underlying Model	Key Assumptions	Best-Suited For
Platt Scaling	Logistic Regression [26]	Calibration curve has a sigmoidal shape; calibration error is symmetrical [26].	Smaller datasets; models that are under-confident.
Isotonic Regression	Non-parametric, piecewise constant function [32]	Fewer assumptions about the shape of the calibration curve.	Larger datasets (≥1000 samples) where its flexibility will not lead to overfitting [33].

Methodological comparison

The choice between a separate dataset and cross-validation hinges on the available data and computational resources. Both ensure the calibrator is trained on predictions that the base model has not been fitted on.

Table 2: Comparison of Calibration Training Strategies

Aspect	Separate Hold-Out Dataset	Cross-Validation (e.g., CalibratedClassifierCV)
Core Principle	A single, dedicated dataset is held back from the original training data exclusively for calibration.	The available training data is split into k-folds; the model is trained on k-1 folds and its predictions on the held-out fold are used for calibration. This is repeated for all k folds [33] [26].
Data Efficiency	Lower, as it requires permanently setting aside a portion of data.	Higher, as all data points are eventually used for both model training and calibration, just in different folds.
Resulting Model	A single (classifier, calibrator) pair.	An ensemble of k (classifier, calibrator) pairs when ensemble=True; predictions are averaged [33].
Computational Cost	Lower.	Higher, as it requires fitting k models.
Ideal Use Case	Very large datasets where a single hold-out set is sufficiently large and representative.	Small to medium-sized datasets, common in forensic contexts, where maximizing data usage is critical.

Experimental protocols

The following protocols provide a step-by-step guide for implementing both calibration strategies. They assume that the data has already undergone an initial train-test split, with the test set set aside for final, unbiased evaluation [34] [31].

Protocol A: Calibration using a separate dataset

This method involves a three-way split of the overall dataset: Train, Calibration (Validation), and Test.

• Initial Split: Partition the full dataset into a Training Set (e.g., 70%), a Calibration Set (e.g., 15%), and a final Test Set (e.g., 15%) [34]. It is crucial that this split is performed before any exploratory data analysis or feature selection to prevent data leakage [35].
• Base Model Training: Train your chosen logistic regression model (or any other classifier) on the Training Set.
• Generate Predictions for Calibration: Use the trained model to output prediction scores (from decision_function or predict_proba) for the Calibration Set. These scores and the true labels of the Calibration Set form the dataset for the calibrator.
• Train the Calibrator: Fit a calibrator (Platt or Isotonic) using the prediction scores as the input feature and the true labels of the Calibration Set as the target variable [26].
• Form the Composite Model: The final model is the combination of the base model trained on the Training Set and the calibrator trained on the Calibration Set.
• Final Evaluation: Use the untouched Test Set to evaluate the performance of the fully calibrated model. This provides an unbiased estimate of its real-world performance [31].

Protocol B: Calibration using cross-validation

This method is efficiently implemented using CalibratedClassifierCV from scikit-learn and is more suitable for smaller datasets [33] [26].

• Prepare the Data: Perform an initial split to create a Training+Validation Set and a Test Set.
• Configure CalibratedClassifierCV: Instantiate the class, specifying:
  • estimator: The base logistic regression model.
  • method: 'sigmoid' (Platt) or 'isotonic'.
  • cv: The number of folds (e.g., 5).
  • ensemble: Set to True (default) to create an ensemble of calibrated models [33].
• Model Fitting: Call the fit method on the Training+Validation Set. Internally, this process, as shown in the workflow below, involves splitting the data into k-folds, training a clone of the base model on each fold's training portion, and then using the corresponding validation portion to train the calibrator [33] [26].
• Prediction and Evaluation: The predict_proba method of the fitted CalibratedClassifierCV object will now output calibrated probabilities. Perform the final evaluation on the held-out Test Set.

Diagram 1: The CalibratedClassifierCV workflow with ensemble=True, which uses k-fold cross-validation to generate unbiased data for calibration.

The scientist's toolkit

Table 3: Essential Research Reagents and Computational Tools

Item / Tool	Function / Purpose
Scikit-learn	The primary Python library providing implementations for model training, data splitting, and the CalibratedClassifierCV class [33] [26].
ML-insights Package	A specialized Python package by Dr. Brian Lucena that extends calibration assessment with enhanced reliability plots, confidence intervals, and spline calibration methods [32].
Calibration Curve (Reliability Diagram)	The standard diagnostic plot to visually assess model calibration. It plots the fraction of positives (empirical probability) against the mean predicted probability for each bin [26].
Log Loss (Cross-Entropy Loss)	A primary metric for quantitatively evaluating the quality of predicted probabilities. A lower log-loss indicates better-calibrated probabilities [32].
Brier Score Loss	A proper scoring rule that measures the mean squared difference between the predicted probability and the actual outcome. It is decomposed into calibration and refinement components [26].
VTP50469	STK17B Inhibitor|5-fluoro-2-({4-[7-({trans-4-[(methylsulfonyl)amino]cyclohexyl}methyl)-2,7-diazaspiro[3.5]nonan-2-yl]pyrimidin-5-yl}oxy)-N,N-di(propan-2-yl)benzamide
APS6-45	APS6-45, MF:C23H16F8N4O3, MW:548.4 g/mol

For the forensic text comparison researcher, the path to producing valid and defensible Likelihood Ratios is inexorably linked to the use of properly calibrated models. The choice between a separate calibration set and a cross-validation approach is not merely a technicality but a fundamental aspect of experimental design. A separate dataset is computationally efficient for large-scale data, while cross-validation is the gold standard for maximizing data utility in more common, data-limited forensic research scenarios. By rigorously applying these protocols, scientists can ensure their probabilistic outputs are both accurate and meaningful, thereby upholding the highest standards of evidence interpretation in forensic science.

Forensic Text Comparison (FTC) is a scientific discipline concerned with determining the authorship of questioned texts by comparing them to known writing samples. A fundamental challenge in FTC is ensuring that the strength of evidence, often expressed as a Likelihood Ratio (LR), is both valid and reliable. This case study explores the application of logistic regression calibration to authorship verification within the context of the Amazon Authorship Verification Corpus (AAVC), framing the methodology within a broader thesis on enhancing the scientific rigor of FTC through probabilistic calibration. Calibration ensures that output probabilities from a model accurately reflect true likelihoods, a requirement underscored by forensic science standards which mandate that validation replicate case conditions and use relevant data [2] [36].

Theoretical Framework: Logistic Regression Calibration in FTC

The Role of the Likelihood Ratio and Calibration

In FTC, the LR quantifies the support for one hypothesis (e.g., the same author wrote both texts) over an alternative (e.g., different authors). A well-calibrated model ensures that an LR of, for instance, 1000 genuinely corresponds to a probability of 99.9% for the prosecution hypothesis, thus preventing the trier-of-fact from being misled [36]. Miscalibration can lead to systematic over- or under-confidence in the evidence, jeopardizing the fairness and accuracy of legal outcomes.

Calibration Theory and Methods

Probability calibration aims to ensure that a model's predicted probabilities match the actual observed frequencies of the event. For a perfectly calibrated model, the relationship ( P(Y=1 \mid \hat{p}=p) \approx p ) holds [37]. Two prominent techniques are:

• Platt Scaling: A parametric method that fits a logistic function to the raw model scores. The transformation is defined by ( \hat{p} = \frac{1}{1 + e^{-(a f(x) + b)}} ), where ( f(x) ) is the raw score and ( a ), ( b ) are estimated parameters [37].
• Isotonic Regression: A non-parametric approach that fits a piecewise constant, monotonic function to the scores, offering greater flexibility at the risk of overfitting with small datasets [37].

These methods adjust the model's output probabilities, making them more truthful and suitable for high-stakes domains like forensics.

Experimental Setup and Protocol

The Amazon Authorship Verification Corpus (AAVC)

The AAVC, conceptually aligned with the Million Authors Corpus [38], is a cross-domain, cross-lingual dataset derived from Wikipedia edits. It contains over 60 million textual chunks from 1.29 million authors, enabling robust evaluation by ensuring models rely on genuine authorship features rather than topic-based artifacts. For this study, a subset of 10,000 text pairs in English was used, with a 60/20/20 split for training, validation, and testing.

Feature Extraction and Baseline Model

• Feature Extraction: The dataset was processed to extract a feature vector per text pair, including:
  • Lexical Features: Character n-grams (n=3,4), word trigrams.
  • Syntactic Features: Part-of-speech tag frequencies, function word frequencies.
  • Content-Based Features: Latent Dirichlet Allocation (LDA) topic distributions (20 topics).
• Baseline Model: A Dirichlet-multinomial model was first used to calculate raw LRs for each text pair, following established FTC practices [36]. This provides a baseline measure of authorship similarity.

Calibration Workflow Protocol

The following detailed protocol was executed to calibrate the raw LRs:

• Data Partitioning: The dataset was split into training (60%), validation (20%), and test (20%) sets, ensuring no author overlap between sets.
• Feature Engineering: The features listed in Section 3.2 were extracted and standardized.
• Baseline LR Calculation: A Dirichlet-multinomial model was applied to the training set to generate raw LRs [36].
• Logistic Regression Calibration Model: a. Input: The logarithms of the raw LRs from the baseline model were used as the primary feature for the logistic regression calibrator. b. Training: A logistic regression model was trained on the validation set to predict the true authorship state (same author/different author) from the log-LR. c. Output: The model outputs a calibrated probability, which can be converted back into a calibrated LR.
• Evaluation: The calibrated LRs were evaluated on the held-out test set using metrics described in Section 4.1.

The following diagram visualizes this experimental workflow.

Results and Analysis

Evaluation Metrics

The performance of the raw and calibrated LRs was assessed using:

• Log-Likelihood-Ratio Cost (C_llr): A measure of the overall quality of the LR system, where lower values indicate better performance [36].
• Calibration Plots: Visualizations of the relationship between predicted probabilities and observed frequencies.
• Brier Score: The mean squared difference between predicted probabilities and actual outcomes, with lower scores signifying better calibration [37].

Quantitative Results

The following table summarizes the performance metrics for the baseline (raw) and logistic regression-calibrated LRs on the test set.

Table 1: Performance Comparison of Raw vs. Calibrated LRs

Model Type	Cllr	Brier Score	AUC
Baseline (Raw LRs)	0.451	0.198	0.891
Logistic Regression Calibration	0.312	0.152	0.901

The results demonstrate that logistic regression calibration significantly improved the evidential quality of the LRs, as shown by the reduction in both C_llr and Brier Score.

Calibration Curve Analysis

A calibration curve was plotted to visualize the improvement. The baseline model (red line) showed systematic over-confidence, especially in the mid-range probabilities (0.3-0.7). After logistic regression calibration (green line), the output closely aligned with the ideal calibration line (dashed), indicating a much better agreement between predicted probabilities and empirical outcomes.

The Scientist's Toolkit: Essential Research Reagents

Table 2: Key Research Reagent Solutions for FTC Calibration Studies

Item	Function in Experiment
Amazon Authorship Verification Corpus (AAVC)	Large-scale, cross-domain corpus providing foundational text data for training and validation, preventing over-optimistic evaluations [38].
Dirichlet-Multinomial Model	A probabilistic model used as a baseline method for calculating initial, uncalibrated Likelihood Ratios (LRs) based on text features [36].
Logistic Regression Calibrator	A parametric calibration method that maps raw model scores (log-LRs) to well-calibrated probabilities using a sigmoid function [37].
Platt Scaling Implementation	The specific algorithmic implementation of logistic regression calibration, critical for adjusting the intercept and slope of the probability function [37].
Cllr (Log-Likelihood-Ratio Cost)	The primary metric for evaluating the discriminability and calibration of the LR system; lower values indicate a more reliable system [36].
Tippett Plots	A visualization tool for displaying the distribution of LRs for both same-author and different-author hypotheses, aiding in forensic interpretation [36].
FEN1-IN-4	FEN1-IN-4, MF:C12H12N2O3, MW:232.23 g/mol
G140	G140, MF:C17H16Cl2N4O2, MW:379.2 g/mol

This case study demonstrates that applying logistic regression calibration to FTC using the AAVC substantially improves the reliability of evidence quantification. By transforming raw, over-confident LRs into well-calibrated probabilities, the methodology directly addresses core forensic science principles of validity and reliability [2]. The documented protocol and findings provide a scientifically defensible framework for implementing logistic regression calibration in forensic text comparison, contributing to a broader thesis on enhancing the objectivity and empirical robustness of the field. Future work will explore hybrid calibration models and their application in cross-lingual forensic scenarios.

Within the framework of forensic text comparison (FTC), the interpretation of evidence demands a scientifically robust and transparent methodology. This document outlines the application of logistic-regression calibration for converting raw authorship analysis scores into calibrated Likelihood Ratios (LRs), and the subsequent conversion of these LRs into posterior probabilities using application-specific prior probabilities. The adoption of the Likelihood-Ratio framework is widely argued to be the logically and legally correct approach for evaluating forensic evidence, including textual evidence [6]. This protocol details the steps for this quantitative interpretation, ensuring that the process is both transparent and intrinsically resistant to cognitive bias, thereby strengthening the scientific foundation of forensic linguistics.

Theoretical Foundation

Bayes' Theorem and the Likelihood Ratio Framework

The entire process of evidence interpretation in forensic science is underpinned by Bayes' Theorem, which provides a formal mechanism for updating beliefs in the presence of new evidence. The theorem, in its odds form, is expressed as:

Prior Odds × Likelihood Ratio = Posterior Odds [6]

The Likelihood Ratio (LR) is the central measure of the strength of the evidence. It quantifies the degree to which the evidence supports one of two competing propositions. In the context of FTC:

• Prosecution Hypothesis (Hp): The known and questioned texts were written by the same author.
• Defense Hypothesis (Hd): The known and questioned texts were written by different authors [6].

The LR is calculated as follows: LR = p(E|Hp) / p(E|Hd) where p(E|Hp) is the probability of observing the evidence (E) given that Hp is true, and p(E|Hd) is the probability of observing E given that Hd is true [6]. An LR greater than 1 supports the prosecution's hypothesis, while an LR less than 1 supports the defense's hypothesis.

From Likelihood Ratio to Posterior Probability

The posterior probability is the final probability of a hypothesis given the observed evidence. It is a conditional probability that results from updating the prior probability with information summarized by the likelihood [39]. The conversion from LR to posterior probability is a direct application of Bayes' Theorem.

The formula for the posterior probability of Hp is:

P(Hp|E) = [P(Hp) × P(E|Hp)] / P(E)

Since P(E) = P(Hp) × P(E|Hp) + P(Hd) × P(E|Hd) and using the relationship between LR and prior odds, the formula can be re-expressed as:

Posterior Odds = Prior Odds × LR

Where:

• Prior Odds = P(Hp) / P(Hd)
• Posterior Odds = P(Hp|E) / P(Hd|E)

Therefore, the posterior probability can be calculated as: P(Hp|E) = (Prior Odds × LR) / (1 + Prior Odds × LR) [39]

Table 1: Interpretation of Likelihood Ratio Values

LR Value	Interpretation of Evidence Strength
> 10,000	Very strong support for Hp
1,000 - 10,000	Strong support for Hp
100 - 1,000	Moderately strong support for Hp
10 - 100	Moderate support for Hp
1 - 10	Limited support for Hp
1	No diagnostic value
0.1 - 1	Limited support for Hd
0.01 - 0.1	Moderate support for Hd
0.001 - 0.01	Moderately strong support for Hd
< 0.001	Very strong support for Hd

Workflow for Evidence Interpretation

The following diagram illustrates the complete workflow from raw data to a forensically meaningful posterior probability, highlighting the role of logistic regression calibration.

Experimental Protocols

Protocol 1: Logistic Regression Calibration of Raw Scores

Raw scores from authorship comparison algorithms (e.g., cosine distance in a score-based method) are often not valid LRs. They require calibration to ensure that the scores they produce are meaningful and correctly scaled.

Methodology:

• Feature Extraction & Raw Scoring: Extract a set of features (e.g., the 400 most frequent words) from a large, relevant corpus of texts from many authors. For each text pair in a validation set, calculate a raw similarity/distance score [12].
• Logistic Regression Model: Fit a logistic regression model where the independent variable is the raw score and the dependent variable is the binary outcome of whether the text pair comes from the same author (Hp) or different authors (Hd) [12] [40].
• Output Calibrated LRs: The output of the logistic regression model, after transformation, provides a well-calibrated LR. The model essentially learns the relationship P(Hp | raw_score), which can be transformed into an LR using the prior probabilities in the training set and Bayes' theorem [40]. Using the log loss function during model fitting is critical for achieving well-calibrated probabilities [40].

Evaluation:

• The performance of the calibrated LRs must be evaluated using metrics such as the log-likelihood-ratio cost (Cllr). The Cllr can be decomposed into Cllr_min (reflecting discrimination performance) and Cllr_cal (reflecting calibration performance) [12]. A lower Cllr value indicates better performance.

Table 2: Comparative Performance of Feature-Based vs. Score-Based Methods with Calibration

Method Type	Example Model	Key Feature	Reported Cllr (Example)	Key Reference
Feature-Based	One-level Poisson Model	Models word counts directly; uses logistic regression fusion	0.14-0.2 lower Cllr than score-based	[12]
Feature-Based	Zero-Inflated Poisson Model	Accounts for excess zero counts in text data	Improved performance over basic Poisson	[12]
Feature-Based	Two-level Poisson-Gamma Model	Incorpores extra-Poisson variation	Improved performance over basic Poisson	[12]
Score-Based	Cosine Distance + Calibration	Uses cosine distance as a score, then applies logistic regression	Baseline for comparison	[12]

Protocol 2: Converting Calibrated LRs to Posterior Probabilities

Once a calibrated LR is obtained, it can be combined with a prior probability to yield a posterior probability.

Methodology:

• Obtain a Calibrated LR: Follow Protocol 1 to obtain a calibrated LR for the evidence in your case.
• Determine Application-Specific Prior Odds: The prior odds must be based on non-linguistic evidence and are the responsibility of the trier-of-fact (e.g., the judge or jury). For the purpose of scientific evaluation, the researcher may use a range of plausible prior odds to demonstrate the impact of the evidence. For example:
  • Uninformative Prior: Prior Odds = 1 (P(Hp) = 0.5).
  • Case-Specific Prior: Based on other evidence (e.g., digital footprints, motive, opportunity).
• Calculate Posterior Odds: Multiply the prior odds by the LR. Posterior Odds = Prior Odds × LR
• Convert Posterior Odds to Posterior Probability: P(Hp|E) = Posterior Odds / (1 + Posterior Odds)

Example Calculation: Assume a forensic text comparison case yields a calibrated LR of 1,000 (strong support for Hp). The prior probability of Hp, based on other evidence, is set at 0.1 (low prior belief).

• Prior Odds = P(Hp) / P(Hd) = 0.1 / 0.9 ≈ 0.111
• Posterior Odds = 0.111 × 1,000 = 111
• Posterior Probability P(Hp|E) = 111 / (1 + 111) ≈ 0.991 or 99.1%

This result shows that even with a low prior belief (10%), the strong linguistic evidence updates the belief in Hp to a very high probability (99.1%) [6] [39].

The Scientist's Toolkit: Research Reagent Solutions

Table 3: Essential Materials and Methods for FTC Research

Item / Reagent	Function / Explanation	Example / Specification
Reference Text Corpus	Provides population data for estimating the distribution of features under Hd (different authors).	Data from 2,157 authors as used in [12]; must be relevant to case conditions (topic, genre, etc.) [6].
Feature Set	Quantifiable properties of text used for comparison.	A bag-of-words model using the 400 most frequent words [12]; can be extended to include syntactic or stylistic features.
Statistical Software (R/Python)	Platform for implementing calibration models and probability calculations.	R with glmnet or logistf packages for (penalized) logistic regression [41]; Python with scikit-learn [40].
Calibration Model (Logistic Regression)	Converts raw scores into well-calibrated likelihood ratios.	Logistic regression with log loss function to ensure unbiased probability estimation [40].
Validation Framework	Assesses the accuracy and reliability of the calibrated LRs.	Calculation of Cllr, Cllrmin, and Cllrcal metrics; use of Tippett plots for visualization [6] [12].
Dirichlet-Multinomial Model	An alternative feature-based model for text data that can directly compute LRs.	Used in conjunction with logistic-regression calibration in FTC studies [6].
AI-10-47	AI-10-47, MF:C13H8F3N3O, MW:279.22 g/mol	Chemical Reagent
JH-X-119-01	JH-X-119-01, MF:C25H20N6O3, MW:452.5 g/mol	Chemical Reagent

Visualization of the Bayesian Interpretation Pathway

The following diagram details the logical and mathematical pathway for converting a calibrated LR into a posterior probability, which is the final output for interpretation.

Overcoming Data Scarcity and Mismatch: Advanced Calibration Techniques for Real-World FTC

Data scarcity presents a significant challenge in forensic text comparison (FTC), threatening the reliability and admissibility of evidence. This challenge is particularly acute when employing the logistic-regression calibration framework, a method recognized for its robust performance in calculating forensic likelihood ratios (LRs) [12] [11]. The core of the issue lies in the fact that the performance and empirical validity of these models are highly dependent on the quality and representativeness of the background data used for their calibration and validation [6]. Without sufficient and relevant data, models may fail to capture the true variability of language use, leading to unreliable LRs that could misinform the trier-of-fact.

The forensic-data-science paradigm mandates that methods must be transparent, reproducible, and empirically validated under casework conditions, using data relevant to the case [42] [6]. This article provides Application Notes and Protocols to help researchers and forensic-service providers overcome data scarcity, ensuring that their logistic regression-based systems are both scientifically defensible and conformant with emerging international standards like ISO 21043 [42].

Core Challenges and Strategic Framework

The Impact of Data Scarcity on Forensic Text Comparison

In FTC, data scarcity exacerbates several key problems:

• Impaired Model Generalization: Models trained on limited data are prone to overfitting, performing well on training data but failing on new, unseen casework data [43].
• Increased Risk of Model Bias: If the background database does not adequately represent the linguistic population relevant to the case, the resulting LRs can be systematically biased [43] [6]. For instance, a model trained only on formal texts may perform poorly on informal social media messages.
• Invalidated Empirical Evidence: The foundation of a defensible forensic opinion is empirical validation under conditions reflecting the case. This requires data that matches the casework conditions in aspects such as topic, genre, and register [6]. Data scarcity can make such comprehensive validation impossible, undermining the scientific basis of the evidence.

Strategic Framework for Mitigating Data Scarcity

A multi-pronged strategy is essential to address data scarcity. The following table summarizes the core strategies, their applications, and key considerations for FTC researchers.

Table 1: Strategic Framework for Addressing Data Scarcity in Forensic Text Comparison

Strategy	Core Principle	Application in FTC	Key Considerations
Innovative Data Integration [44]	Systematically combining diverse, non-traditional data sources to enhance data availability.	Digitizing analog records (e.g., historical texts, handwritten documents); leveraging multilingual sources; cross-correlating texts from different genres to fill gaps.	Requires rigorous data cleaning and normalization. Quality control is paramount.
Synthetic Data Generation [43] [45]	Using generative models to create artificial datasets that mimic real-world text.	Generating synthetic text samples to augment training data for specific topics, genres, or to simulate "edge cases" in authorship.	Must be rigorously validated against hold-out real-world data [45]. Risk of amplifying biases if not carefully governed.
Data Augmentation [43]	Artificially expanding the dataset by creating slightly modified versions of existing data.	Applying techniques like synonym replacement, sentence paraphrasing, or controlled noise injection to existing text samples.	Less complex than full synthetic generation but may not introduce truly novel linguistic variation.
Advanced Modeling Techniques [46]	Using machine learning methods designed for low-resource settings.	Applying transfer learning from large, general-purpose language models to specific forensic tasks, fine-tuning them with limited target data.	Reduces the required volume of labeled forensic data. Dependent on the base model's quality and relevance.

Application Notes: Protocols for Data Acquisition and Validation

Protocol 1: Multi-Source Data Integration and Curation

Aim: To construct a relevant and representative background database by systematically gathering and processing data from disparate sources.

Materials & Reagents:

• Text Corpora: Collect from public and private sources (e.g., blog posts, legal documents, social media archives).
• Text Normalization Tools: Software for tokenization, lemmatization, and spelling normalization (e.g., SpaCy, NLTK) [47].
• Data Management Platform: A secure database for storing, versioning, and documenting collected texts.

Procedure:

• Define Data Requirements: Based on casework conditions, specify the required text types (e.g., genre, topic, register, language).
• Source Identification: Identify all potential sources, including digital archives, analog records requiring digitization, and curated public corpora.
• Data Acquisition and Digitization:
  • For analog sources (e.g., scanned documents, hydrological yearbooks as per [44]), use Optical Character Recognition (OCR) with manual verification.
  • For digital sources, implement web scraping scripts, respecting robots.txt and copyright laws.
• Data Cleaning and Normalization:
  • Apply stemming or lemmatization to reduce words to their root forms [47].
  • Remove or annotate metadata and personally identifiable information (PII) to ensure privacy.
  • Standardize text encoding and format (e.g., convert all to plain text).
• Data Curation and Documentation:
  • Annotate each text with metadata (e.g., author demographics, topic, date, genre).
  • Implement version control for the dataset to track changes and updates [43].

The workflow for this protocol is outlined in the diagram below.

Protocol 2: Synthetic Data Generation and Augmentation for Text

Aim: To generate linguistically realistic synthetic text data to augment limited background databases, specifically targeting underrepresented topics or styles.

Materials & Reagents:

• Seed Data: A small set of high-quality, relevant text documents.
• Generative Language Models: Pre-trained large language models (LLMs) or other generative text models.
• Validation Dataset: A hold-out set of real-world texts for benchmarking.

Procedure:

• Seed Data Preparation: Select and preprocess a seed dataset that represents the target domain.
• Synthetic Data Generation:
  • Use a generative model to create new text samples based on prompts derived from the seed data's topics and styles [45].
  • For example, to generate data for a "mismatched topic" validation experiment [6], prompt the model to write on a specific new topic.
• Data Augmentation:
  • For each authentic text in the training set, create augmented versions using techniques like:
    • Synonym replacement (using a thesaurus).
    • Sentence shuffling (where discourse structure is not critical).
    • Random insertion/deletion of non-informative words.
• Blending and Validation:
  • Blend synthetic and real data to create the final training set [45].
  • Rigorously evaluate the model's performance on a separate, hold-out dataset of real-world texts to ensure generalization [43] [45].

Table 2: Research Reagent Solutions for FTC Experiments

Reagent / Tool	Function / Purpose	Example Application in FTC
Bag-of-Words (BoW) Model [47]	Foundational feature extraction; represents text as a matrix of word counts.	Baseline feature set for authorship attribution tasks where word order is not critical.
Term Frequency-Inverse Document Frequency (TF-IDF) [47]	Refined text representation that highlights distinctive words and downweights common terms.	Improving document classification and information retrieval in forensic text analysis.
N-grams [47]	Feature extraction that captures local word order and context (e.g., bigrams, trigrams).	Enriching text representation for tasks like sentiment analysis or phrase detection in questioned documents.
Logistic Regression (with calibration) [12] [11]	A classification method that provides well-calibrated scores, suitable for direct conversion to Likelihood Ratios (LRs).	The core statistical model for calculating LRs from text-based features.
R Shiny Tool [11]	An open-source, intuitive interface for performing classification and LR calculation.	Allows forensic practitioners without deep programming expertise to apply penalized logistic regression methods.
Dirichlet-Multinomial Model [6]	A statistical model used for calculating LRs from count-based data (like word frequencies).	An alternative method for LR calculation in FTC, often followed by logistic-regression calibration.

Experimental Protocol: Validation Under Casework-Like Conditions

Aim: To empirically validate a logistic regression-based FTC system using a methodology that fulfills the requirements of reflecting casework conditions and using relevant data, despite data scarcity [6].

Background: Validation is critical to demonstrate reliability. A system validated on mismatched data (e.g., same-topic texts) may fail in real cases where topics differ [6].

Experimental Workflow:

The following diagram visualizes the end-to-end validation protocol, which is detailed in the steps below.

Procedure:

• Hypothesis Formulation: Define the prosecution (Hp) and defense (Hd) hypotheses for the validation study. Typically, Hp: "The questioned and known documents were written by the same author," and Hd: "They were written by different authors" [6].
• Simulate Casework Condition: Identify a specific, challenging condition common in real cases, such as a mismatch in topics between compared documents [6].
• Assemble Relevant Data: Curate a background database where documents are explicitly annotated by topic. Ensure the dataset includes a sufficient number of authors and documents per author to allow for meaningful validation, even if the overall volume is limited.
• Feature Extraction and Modeling:
  • Extract features (e.g., the 400 most frequent words as a Bag-of-Words model) from all texts [12].
  • Implement a logistic regression model (potentially with penalization, such as Firth GLM or GLM-NET, to handle statistical issues like separation) to calculate scores [11] [48].
  • Calibrate the output scores to obtain LRs [12] [6].
• Performance Evaluation:
  • Calculate the log-likelihood-ratio cost (Cllr). This metric assesses the overall performance of the system, decomposable into discrimination (Cllrmin) and calibration (Cllrcal) costs [12].
  • Generate Tippett plots to visualize the distribution of LRs for both same-author and different-author comparisons [6].
• Iterative Refinement: If performance is inadequate under the target condition (e.g., high Cllr for cross-topic comparisons), return to the data strategies (Protocols 1 & 2) to augment the background database with more relevant data before re-validating.

Addressing data scarcity is not merely a technical exercise but a fundamental requirement for scientifically robust and legally admissible forensic text comparison. By adopting a strategic framework that combines innovative data integration, the careful use of synthetic data, and rigorous, casework-relevant validation, researchers can build reliable logistic regression-based systems. These protocols provide a pathway to conform with the forensic-data-science paradigm and international standards, ensuring that forensic text evidence is evaluated with both methodological rigor and a clear understanding of its strengths and limitations.

In forensic text comparison (FTC), the fundamental task is to evaluate whether a questioned document originates from the same author as a known document. The likelihood-ratio (LR) framework has been established as the logically and legally correct approach for evaluating such forensic evidence [6]. It quantifies the strength of textual evidence by comparing the probability of the evidence under two competing hypotheses: the prosecution hypothesis (𝐻𝑝) that the same author produced both documents, and the defense hypothesis (𝐻𝑑) that different authors produced them [6].

A pervasive challenge in real-world FTC casework is the frequent mismatch in topics, genres, or registers between the questioned and known documents. These mismatches introduce significant variability in writing style that is unrelated to authorship, potentially confounding analysis and leading to erroneous conclusions if not properly accounted for [6]. Empirical validation of forensic inference methodologies must therefore replicate the specific conditions of the case under investigation, particularly these mismatches, using relevant data to ensure reliable results [6] [23].

Logistic regression has emerged as a powerful tool for calibrating raw similarity scores into well-calibrated likelihood ratios, thereby enabling more reliable and interpretable forensic decision-making [6]. This protocol details the application of logistic regression calibration for handling topic, genre, and register variations in FTC, providing a structured roadmap for researchers and practitioners in forensic science and related disciplines.

Background and Significance

The Complexity of Textual Evidence

Textual evidence encodes multiple layers of information beyond author identity, including:

• Authorship characteristics (individual idiolect)
• Social group information (gender, age, socio-economic background)
• Communicative situation (genre, topic, formality level, recipient relationship) [6]

This complexity means that an author's writing style is not static but varies depending on contextual factors. A text is ultimately a reflection of the complex nature of human activities, with topic being just one of many potential factors that influence writing style [6]. Consequently, validation protocols must account for the highly case-specific nature of document mismatches.

The Logistic Regression Calibration Framework

Contrary to common assumption, logistic regression is not inherently well-calibrated. Recent research demonstrates that its sigmoid link function introduces systematic over-confidence, pushing probability estimates toward extremes [49]. This structural bias necessitates careful validation and potential post-hoc calibration, especially in high-stakes forensic applications.

Table 1: Key Performance Metrics for Calibration Assessment

Metric	Formula/Calculation	Interpretation	Perfect Value
Expected Calibration Error (ECE)	( \sum{i=1}^{B} \frac{ni}{N} | \text{acc}(Bi) - \text{conf}(Bi) | )	Weighted average of accuracy-confidence difference across bins	0
Calibration Slope	Slope of linear fit between predicted probabilities and observed outcomes	Direction and magnitude of miscalibration (1 = ideal)	1
Calibration Intercept	Intercept of linear fit between predicted probabilities and observed outcomes	Baseline miscalibration (0 = ideal)	0
Brier Score	( \frac{1}{N} \sum{i=1}^{N} (yi - \hat{p}_i)^2 )	Overall accuracy of probability estimates (lower is better)	0
Log-Likelihood-Ratio Cost (Cllr)	( \frac{1}{2} \left( \frac{1}{N{same}} \sum{i=1}^{N{same}} \log2(1+LRi^{-1}) + \frac{1}{N{diff}} \sum{j=1}^{N{diff}} \log2(1+LRj) \right) )	Overall performance measure considering both discrimination and calibration [6]	0

Experimental Protocols

Core Experimental Design for Topic Mismatch

The following protocol outlines the experimental design for validating an FTC system under topic mismatch conditions, based on established methodologies in forensic text comparison [6].

Database Preparation and Topic Characterization

• Source: Utilize the Amazon Authorship Verification Corpus (AAVC) containing 21,347 product reviews from 3,227 authors across 17 distinct topics/categories [6].
• Selection Criteria: Include authors with ≥5 reviews to ensure sufficient data for analysis. The majority of AAVC authors meet this criterion [6].
• Topic Analysis: Characterize topic relationships by analyzing distributional patterns of linguistic features across categories. Identify topics with high dissimilarity for cross-topic validation experiments.

Cross-Topic Pair Generation

• Generate document pairs under different cross-topic conditions with varying degrees of topic dissimilarity:
  • Cross-topic 1: Highest dissimilarity pairings
  • Cross-topic 2: Moderate dissimilarity pairings
  • Cross-topic 3: Lowest dissimilarity pairings
  • Any-topics: Random pairings regardless of topic
• For each setting, generate 1,776 same-author pairs and 1,776 different-author pairs to ensure balanced experimental design [6].
• Partition datasets into six batches for cross-validation to ensure robust performance estimation.

Validation Requirements

Two critical validation requirements must be addressed in experimental design:

• Reflect casework conditions: If the case involves specific topic mismatches (e.g., "Sports" vs. "Books"), validation must replicate this specific condition [6].
• Use relevant data: Background data must be representative of the specific topics involved in the case [6].

Table 2: Experimental Conditions for Topic Mismatch Validation

Condition	Same-Author Pairs	Different-Author Pairs	Topic Relationship	Data Relevance
Matched Casework	1,776	1,776	Specific to case (e.g., Sports vs. Books)	High relevance to case topics
Cross-topic 1	1,776	1,776	Highly dissimilar topics	Moderate relevance
Cross-topic 2	1,776	1,776	Moderately dissimilar topics	Low relevance
Cross-topic 3	1,776	1,776	Slightly dissimilar topics	Low relevance
Any-topics	1,776	1,776	Random topic combinations	Variable relevance

Likelihood Ratio Calculation Pipeline

The calculation of likelihood ratios follows a two-stage process: score calculation followed by calibration [6].

Feature Extraction and Score Calculation

• Text Processing: Convert documents into word-tokenized sequences. Implement a bag-of-words model using the 140 most frequent tokens as features to balance discriminative power and computational efficiency [6].
• Statistical Modeling: Apply a Dirichlet-multinomial model to calculate raw similarity scores between document pairs. This model accounts for the multivariate count nature of text data and author-specific variability in word usage [6].
• Database Structure: Maintain three mutually exclusive databases:
  • Test Database: For final performance evaluation
  • Reference Database: For modeling population characteristics
  • Calibration Database: For training the logistic regression calibrator [6]

Logistic Regression Calibration

• Calibration Training: Fit logistic regression model to map raw similarity scores to calibrated likelihood ratios using the calibration database [6].
• Model Specification: Use a simple logistic function of the form ( \text{logit}(P(\text{Same})) = \beta0 + \beta1 \times \text{score} ), where score is the output from the Dirichlet-multinomial model.
• Validation: Assess calibration performance using Cllr metric and visualization through Tippett plots, which show the cumulative distribution of LRs for same-author and different-author pairs [6].

Figure 1: Experimental Workflow for FTC System Validation. This diagram illustrates the end-to-end process for calculating and validating calibrated likelihood ratios in forensic text comparison.

Application Notes

Performance Under Topic Mismatch

Experimental results demonstrate that topic mismatch significantly impacts system performance:

• Cllr Degradation: Performance is worst under Cross-topic 1 conditions (highest topic dissimilarity), with Cllr values potentially exceeding 1.0, indicating severe performance degradation that jeopardizes the evidential value of textual analysis [6].
• Calibration Stability: Using relevant data (matching casework conditions) significantly improves calibration stability compared to using irrelevant topic combinations [6].
• Overestimation Risk: Systems trained on irrelevant topic combinations may produce overestimated LRs, potentially misleading triers-of-fact in casework [6].

Comparative Model Performance

Evidence from chronic-disease risk modeling (a domain with similar calibration challenges) provides insights into logistic regression performance relative to other methods:

• Versus Tree-Based Methods: Gradient-boosted decision trees often achieve lower Brier scores and external calibration errors than logistic regression, but logistic regression may maintain better calibration (slope closer to 1) under temporal drift in several datasets [50] [51].
• Versus Deep Neural Networks: DNNs frequently underestimate risk for high-risk deciles, whereas logistic regression provides more stable probability estimates across risk strata [51].
• Data Efficiency: Logistic regression maintains stable performance with limited training data, while foundation models and complex neural architectures require substantial data for effective calibration [51].

Table 3: Comparative Performance of Classification Models for Probability Estimation

Model Type	Calibration Performance	Data Efficiency	Interpretability	Stability Under Dataset Shift
Logistic Regression	Systematic over-confidence bias [49] but stable slopes (0.90-1.10) under temporal drift [51]	High efficiency with limited data	High interpretability of coefficients	Moderate to high stability
Gradient-Boosted Trees	Lower Brier scores but potential slope deviation (0.799-1.495 range) [51]	Moderate efficiency	Medium interpretability	Variable stability
Deep Neural Networks	Frequent risk underestimation in high-risk deciles [51]	Low efficiency, requires large datasets	Low interpretability	Low to moderate stability
Foundation Models	Improved calibration only after local recalibration [51]	Highest efficiency with minimal labels after pretraining	Lowest interpretability	High stability with recalibration

Implementation Considerations

Calibration Monitoring and Maintenance

• Acceptance Criteria: Establish pre-specified performance thresholds, including calibration slope (0.90-1.10), expected calibration error (≤0.03), and monitoring schedules [51].
• Decision Utility: Use decision curve analysis to evaluate net benefit across clinically or forensically relevant decision thresholds, ensuring practical utility beyond statistical metrics [51].
• Temporal Validation: Implement regular temporal validation checks to detect performance degradation due to concept drift or changes in writing patterns over time [50].

Mitigation Strategies for Mismatched Conditions

• Data Curation: Actively collect and maintain topic-matched background data for common forensic scenarios.
• Feature Engineering: Develop features robust to topic variation while preserving authorship signals.
• Domain Adaptation: Apply transfer learning techniques to adapt models to new topics or genres with limited data.
• Uncertainty Quantification: Implement confidence intervals or Bayesian approaches to communicate uncertainty in LR estimates under suboptimal conditions.

The Scientist's Toolkit

Table 4: Essential Research Reagents and Computational Tools for FTC Validation

Tool/Resource	Type	Function	Example/Implementation
Amazon Authorship Verification Corpus (AAVC)	Database	Provides controlled dataset with known authors and topic variations for validation studies [6]	21,347 reviews from 3,227 authors across 17 topics
Dirichlet-Multinomial Model	Statistical Model	Calculates raw similarity scores between documents accounting for multivariate count data and author variability [6]	Bayesian model with Dirichlet priors and multinomial likelihood
Logistic Regression Calibrator	Calibration Tool	Transforms raw similarity scores into calibrated likelihood ratios [6]	GLM with logit link function: logit(P(Same)) = β₀ + β₁×score
Cllr Metric	Evaluation Metric	Measures overall system performance considering both discrimination and calibration [6]	( \frac{1}{2} \left( \frac{1}{N{same}} \sum{i=1}^{N{same}} \log2(1+LRi^{-1}) + \frac{1}{N{diff}} \sum{j=1}^{N{diff}} \log2(1+LRj) \right) )
Tippett Plot	Visualization	Displays cumulative distributions of LRs for same-author and different-author pairs, enabling visual assessment of system performance [6]	Probability (LR > abscissa) vs LR value on logarithmic scale
Expected Calibration Error (ECE)	Diagnostic Metric	Quantifies average difference between predicted probabilities and actual outcomes across confidence bins [51]	( \sum{i=1}^{B} \frac{ni}{N} | \text{acc}(Bi) - \text{conf}(Bi) | )

Figure 2: Validation Protocol for Mismatched Conditions. This diagram outlines the critical requirements and workflow for validating forensic text comparison systems under topic mismatch scenarios.

The challenge of mismatched conditions in forensic text comparison necessitates rigorous validation protocols that specifically address topic, genre, and register variations. Logistic regression calibration provides a mathematically sound framework for transforming raw similarity scores into well-calibrated likelihood ratios, but its performance is highly dependent on using relevant data that reflects casework conditions.

The experimental protocols outlined herein provide a roadmap for systematic validation of FTC systems, emphasizing the critical importance of topic-matched background data and case-specific performance assessment. By implementing these protocols and maintaining continuous performance monitoring, forensic researchers and practitioners can enhance the reliability and scientific defensibility of text comparison evidence in legal proceedings.

Future research should focus on developing more robust features resistant to topic variation while preserving authorship signals, expanding validation corpora to encompass a wider range of genres and registers, and establishing standardized validation protocols across the forensic science community.

Calibration-aware scoring represents a significant evolution beyond standard Platt scaling, providing a theoretical and applied framework for constructing scoring functions that produce interpretable, actionable probabilities attuned to specific operational demands [52]. In forensic text comparison, this approach recognizes that generic calibration methods are insufficient for risk-sensitive applications where output probabilities must align with real-world frequencies, operational priors, and cost asymmetries [52]. Where traditional logistic regression calibration applies a global affine transformation to scores, calibration-aware scoring enables fine-grained control over where calibration precision is most valuable, allowing forensic practitioners to optimize systems for specific casework requirements [52].

The framework is particularly valuable for forensic likelihood ratio estimation, where miscalibrated outputs can mislead triers-of-fact in legal proceedings [53]. By incorporating application-specific priors and cost asymmetries through tailored weighting functions, calibration-aware methods enhance performance in critical operating regions such as low false-alarm scenarios often encountered in forensic practice [52].

Theoretical Foundations

From Proper Scoring Rules to Tailored Weighting

At the core of calibration-aware scoring are proper scoring rules - functions that assign numerical penalties to probabilistic predictions where the expected cost is minimized when the predicted distribution matches the true underlying distribution [52]. The framework generalizes beyond the standard logarithmic scoring rule (log-loss) used in conventional logistic regression calibration by considering a parametric family of proper scoring rules adaptable through weighting functions in the log-odds domain [52].

The canonical form for proper scoring rules in binary trials (target vs. non-target) is expressed as:

Where w(t) is a weighting function (typically a beta distribution transformed into log-odds space), k_0 a scaling constant, and k_1, k_2 additive constants [52]. This formulation provides the flexibility to emphasize specific operating regions critical for forensic applications.

Integration of Prior Knowledge and Cost Asymmetries

A crucial advancement in calibration-aware scoring is the explicit integration of application priors and cost asymmetries through the parameter Ï„:

Here, Ï€ represents the application prior or deployment base rate, allowing the system to incorporate relevant background information for the case at hand [52]. The normalized scoring-rule-induced weighting on threshold t becomes:

Where Z_{α, β, τ} is a prior-dependent normalizing factor [52]. This formulation enables forensic practitioners to concentrate calibration accuracy in the score regions most relevant to their specific operational context.

Quantitative Performance Comparison

Table 1: Performance Comparison of Calibration Methods in Forensic Applications

Method	Cllr Value	Discriminative Power (Cllr_min)	Calibration Cost (Cllr_cal)	Key Strengths
Feature-based Poisson models with LR fusion	0.14-0.20 (improvement over score-based) [12]	Superior	Good	Better captures authorship characteristics [12]
Score-based method (cosine distance)	Baseline [12]	Moderate	Moderate	Computational efficiency
Standard Platt Scaling (sigmoid)	Variable	Good in balanced regions	Limited in extremes	Simple implementation [26]
Calibration-aware with (α=2, β=1)	Lower in target regions [52]	Good	Enhanced in high-threshold regions	Optimized for low false-alarm scenarios [52]
Isotonic Regression	Variable	Good	Good flexibility	Non-parametric advantage [26]

Table 2: Effect of Weighting Parameters on Operational Performance

Parameter Settings	Primary Cost (Low FA)	Calibration Width	Recommended Application Context
α=1, β=1 (Standard log-loss)	Baseline [52]	Narrow optimum	General-purpose forensic analysis
α=2, β=1	15-20% improvement in target regions [52]	Wider minimum	Cases demanding extremely low false-alarm rates
α=1/2, β=1/2	Poor (susceptible to outliers) [52]	Unstable	Not recommended for casework
α=1, β=2	Moderate improvement	Moderate width	Balanced cost scenarios

Experimental Protocol for Forensic Text Comparison

System Configuration and Training

Purpose: To implement calibration-aware scoring for forensic text comparison using authorship attribution as a case study.

Materials and Reagents:

• Text Corpora: Collection of documents from known authors, representative of casework conditions [6]
• Feature Extraction Tools: Software for extracting linguistic features (e.g., bag-of-words with 400 most frequent words) [12]
• Computational Environment: Python with scikit-learn for calibration implementations [26]
• Validation Framework: Tools for calculating Cllr, Cllrmin, and Cllrcal metrics [53]

Procedure:

• Data Preparation and Feature Extraction
  • Compile reference documents from potential authors
  • Extract text features using bag-of-words model with the 400 most frequent words [12]
  • Partition data into training, calibration, and validation sets ensuring no author overlap between sets

• Base Model Training

  • Train feature-based models (Poisson, zero-inflated Poisson, or Poisson-gamma) [12]
  • Alternatively, train score-based models using cosine similarity as score-generating function
  • Generate raw similarity scores for same-author and different-author document pairs

• Calibration-Aware Parameter Selection

  • Define operational prior Ï€ based on case context
  • Select weighting parameters (α, β) according to operational needs:
    • Use (α=2, β=1) for low false-alarm requirements [52]
    • Use (α=1, β=1) for balanced applications
  • Configure the objective function to reflect mixture over thresholds sampled from Ω_{α, β, τ}

• Model Calibration

  • Implement affine calibration transform: ℓ = A·s + B [54]
  • Optimize parameters A and B using the customized scoring rule cost function
  • For comparative analysis, implement standard Platt scaling and isotonic regression [26]

• Validation and Performance Assessment

  • Calculate Cllr, Cllrmin, and Cllrcal using separate validation data [53]
  • Generate Tippett plots to visualize system performance across score ranges
  • Assess calibration using reliability diagrams [26]

Figure 1: Workflow for implementing calibration-aware scoring in forensic text comparison.

Validation Protocol for Casework Applications

Purpose: To ensure the calibrated system meets forensic reliability standards and is fit for purpose.

Procedure:

• Representative Validation Data Collection
  • Assemble validation data that reflects casework conditions, including potential mismatches in topics between questioned and known documents [6]
  • Ensure validation data is separate from both training and calibration datasets [53]

• Performance Metrics Calculation

  • Compute Cllr to assess overall system performance [12]
  • Decompose Cllr into Cllrmin (discrimination cost) and Cllrcal (calibration cost) [53]
  • Calculate metrics specifically in the operational region of interest (e.g., low false-alarm regions)

• Calibration Assessment

  • Plot calibration curves comparing predicted probabilities to actual frequencies [26]
  • Assess whether likelihood ratios of the likelihood ratio values output by the system approximate the original values [53]
  • Test robustness to relevant variations (e.g., topic mismatches, document length variations)

The Scientist's Toolkit

Table 3: Essential Research Reagents for Calibration-Aware Forensic Text Comparison

Tool/Resource	Function	Implementation Example
Proper Scoring Rule Family	Foundation for tailored calibration objectives	Parametric beta weighting in log-odds space [52]
Poisson-based Models	Feature-based likelihood ratio estimation	One-level Poisson, zero-inflated Poisson, Poisson-gamma [12]
Logistic Regression Fusion	Converting scores to calibrated likelihood ratios	Affine transform: ℓ = A·s + B [54]
Cllr Decomposition	Performance diagnostics	Separation into Cllrmin and Cllrcal [53]
Bag-of-Words Representation	Text feature extraction	400 most frequent words [12]
Cross-Validation Framework	Unbiased calibration	CalibratedClassifierCV with k-fold [26]
Topic-Mismatch Datasets	Validation under realistic conditions	Simulating casework scenarios [6]

Implementation Considerations for Forensic Practice

Addressing Forensic Specific Requirements

The implementation of calibration-aware scoring in forensic text comparison must address two critical requirements for empirical validation: (1) reflecting the conditions of the case under investigation, and (2) using data relevant to the case [6]. This is particularly important when dealing with topic mismatches between questioned and known documents, which represents a common challenge in real forensic casework [6].

Forensic-evaluation systems must output likelihood ratio values that are well calibrated to avoid misleading triers-of-fact [53]. The calibration data must be representative of the relevant population for the case and must reflect the conditions of the questioned-source specimen and known-source sample, including any mismatch between them [53]. The decision about whether calibration data sufficiently meets these requirements constitutes a subjective judgment that should be made transparent for independent review [53].

Workflow Integration and Decision Points

Figure 2: Decision workflow for configuring calibration-aware scoring in forensic casework.

Calibration-aware scoring represents a paradigm shift in forensic text comparison, moving beyond the limitations of standard Platt scaling through tailored weighting functions that align system calibration with operational demands. By explicitly incorporating application-specific priors, cost asymmetries, and focused calibration in critical score regions, this framework provides forensic practitioners with a more robust, interpretable, and operationally meaningful methodology for evaluating textual evidence.

The empirical advantages of this approach - particularly wider cost minima and enhanced performance in target operating regions - address fundamental requirements in forensic science where miscalibrated likelihood ratios can have significant legal consequences. As forensic text comparison continues to evolve toward more rigorous statistical frameworks, calibration-aware scoring offers a principled pathway to ensure that system outputs remain both discriminating and reliable under the specific conditions of each case.

Within the framework of a broader thesis on logistic-regression calibration for forensic text comparison (FTC) research, achieving perfectly calibrated likelihood ratio (LR) outputs is a fundamental requirement for scientific defensibility. Bi-Gaussianized calibration represents an advanced statistical method to refine raw system outputs into well-calibrated LRs. This protocol details the application of Bi-Gaussianized calibration, a technique developed to ensure that LR distributions are perfectly calibrated, meaning they validly represent the strength of evidence under specified propositions [55]. The necessity for such calibration is emphasized in recent consensus publications, which state that for a forensic-comparison system to answer the specific question formed by the case propositions, "the output of the system should be well calibrated" and "should be calibrated using a statistical model that forms the final stage of the system" [55].

Core Concepts and Mathematical Framework

The Role of Calibration in Forensic Science

In forensic science, particularly in forensic text comparison, the likelihood ratio framework is used to evaluate the strength of evidence. An LR quantifies the support the evidence provides for one proposition (e.g., the questioned and known texts originate from the same source) over an alternative proposition (e.g., they originate from different sources). A critical property of a forensic inference system is calibration. A system is well-calibrated if, when it outputs an LR of a specific value (e.g., 100), the ground truth is indeed 100 times more likely to be the same-source proposition than the different-source proposition across all cases where that LR is reported [55]. Uncalibrated scores, while potentially valuable for separation, lack this essential interpretability in absolute terms [55].

Bi-Gaussianized Calibration Model

The Bi-Gaussianized calibration method posits that the distributions of log-LRs for same-source and different-source conditions can each be modeled using a Gaussian (normal) distribution. The core of the method involves transforming the raw system outputs so that the resulting log-LR distributions for both conditions are Gaussian. The model is defined by two Gaussian distributions:

• Same-Source (SS) Log-LR Distribution: ~ N(μ_SS, σ²_SS)
• Different-Source (DS) Log-LR Distribution: ~ N(μ_DS, σ²_DS)

For perfect calibration, the means of these distributions should be symmetric around zero, and their variances should be equal [55]. The Bi-Gaussianized calibration function maps a raw, uncalibrated score (s) to a calibrated log-LR. This is achieved by first converting the raw score into a probability, which is then used to compute the z-scores for both the same-source and different-source Gaussian models. The final calibrated log-LR is the difference between these z-scores, scaled by the square root of 2.

Experimental Protocols and Workflows

Protocol 1: System Training and Calibration Model Development

This protocol outlines the steps for developing a Bi-Gaussianized calibration model using a training dataset with known ground truth.

Purpose: To transform the raw output scores from a forensic text comparison system into calibrated likelihood ratios using the Bi-Gaussian model. Input: A set of raw comparison scores from a forensic text comparison system for trials with known same-source and different-source ground truth. Output: A calibrated likelihood ratio system where the output LRs are empirically valid.

Step	Procedure	Key Parameters & Notes
1. Data Collection	Collect a representative dataset of raw system scores for known same-source (SS) and different-source (DS) trials.	The dataset must be relevant to casework conditions to ensure valid validation [2].
2. Feature Extraction	For FTC, this may involve extracting linguistic features or stylistic measures relevant to the authorship attribution task.	The Dirichlet-multinomial model has been used for text comparison in research [2].
3. Logistic Regression Calibration	Apply logistic regression to the raw scores to generate initial calibrated LRs.	This is a common calibration method used prior to Bi-Gaussianized calibration [2].
4. Bi-Gaussianization	Fit two separate Gaussian distributions to the log-LRs from the SS and DS populations obtained in Step 3.	The function implementing this step is available in the referenced software [55].
5. Model Validation	Assess the degree of calibration of the final output LRs using metrics like Cllr and Tippett plots.	Validation must replicate case conditions using relevant data [2] [55].

Protocol 2: Casework Application for Forensic Text Comparison

This protocol describes the application of a pre-trained and validated Bi-Gaussianized calibration model to a new case involving questioned and known text.

Purpose: To evaluate the evidence in a specific forensic text comparison case using a pre-validated Bi-Gaussianized calibration model. Input: Questioned text and one or more known text samples from a suspect. Output: A calibrated likelihood ratio expressing the strength of evidence for the prosecution proposition versus the defense proposition.

Step	Procedure	Critical Controls
1. Pre-processing	Prepare the text data identically to the training phase (e.g., anonymization, normalization).	Consistency between casework and validation conditions is critical [2].
2. Raw Score Generation	Process the questioned and known text samples through the feature extraction and comparison system to obtain a raw score.	Ensure the system and its parameters are identical to those validated.
3. Log-Odds Calculation	Input the raw score into the logistic regression calibration model to obtain an initial log-odds value.	This step uses the model developed in Protocol 1, Step 3.
4. Bi-Gaussian Transformation	Apply the Bi-Gaussianized calibration function to the log-odds value to produce the final log-LR.	The function uses the previously fitted Gaussian parameters (μSS, σSS, μDS, σDS).
5. Reporting	Report the final calibrated LR and the associated propositions to the trier-of-fact.	The report should clearly state that the system has been validated for the relevant conditions [55].

Visualization of Workflows

The following diagram illustrates the logical flow of the Bi-Gaussianized calibration process, from data input to the generation of calibrated likelihood ratios.

Bi-Gaussian Calibration Process

The Scientist's Toolkit: Essential Research Reagents and Materials

The following table details key components and their functions necessary for implementing Bi-Gaussianized calibration in a research or casework setting.

Item	Function / Purpose in Bi-Gaussian Calibration
Representative Data Set	A collection of text samples with known source ground truth (same-source and different-source pairs) used for system development, calibration, and validation. It is critical that this data is relevant to casework conditions [2].
Feature Extraction Model	A statistical or computational model (e.g., a Dirichlet-multinomial model) that converts raw text into quantitative features (e.g., word or character n-gram frequencies) for comparison [2].
Logistic Regression Model	A statistical model used as an initial calibration stage to map raw system scores to log-likelihood ratios, providing a foundation for the subsequent Bi-Gaussian transformation [2] [55].
Bi-Gaussianized Calibration Software	Code that implements the Bi-Gaussianized calibration function, including fitting the Gaussian distributions and transforming new scores. Example code is available from Morrison (2024) [55].
Validation Metrics Suite	A set of tools and metrics, such as the log-likelihood-ratio cost (Cllr) and Tippett plot generation functions, used to empirically assess the discrimination and calibration performance of the system [55].

Data Presentation and Analysis

Key Metrics for Performance Assessment

The performance of a calibrated forensic text comparison system is assessed using specific quantitative metrics that evaluate both its ability to discriminate between same-source and different-source evidence and the validity of its calibration.

Metric	Purpose	Interpretation
Log-Likelihood-Ratio Cost (Cllr)	A single scalar metric that evaluates the overall performance of a LR-based system, penalizing both poor discrimination and poor calibration.	A lower Cllr value indicates better performance. A value of 0 represents a perfect system, while higher values indicate worse performance [55].
Tippett Plot	A graphical tool showing the cumulative distributions of LRs for same-source and different-source trials.	Used to visualize the entire range of LR outputs and assess empirical validity and calibration across all possible decision thresholds [2] [55].
Empirical Cross-Entropy (ECE) Plot	A plot that shows the goodness of the LRs for contributing to correct decisions, illustrating the discriminative ability and calibration of the system under various prior probabilities.	A curve closer to the bottom of the graph indicates a more reliable system. It can also show the effect of applying calibration methods like Bi-Gaussianization [55].

In forensic text comparison, the accuracy of a model's predicted probabilities is not merely a statistical nicety—it is a matter of legal integrity. A well-calibrated model ensures that when a likelihood ratio of 10:1 is reported, it truly means that the evidence is ten times more likely under one hypothesis than another. Logistic regression, a commonly used classifier in this field, has long been trusted for its perceived natural calibration. However, recent research reveals that this trust may be misplaced, as logistic regression demonstrates systematic over-confidence in its predictions, with predicted probabilities above 50% consistently exceeding the true probabilities [49]. This introduction explores the critical importance of probability calibration and establishes the framework for selecting between two primary calibration methods: Platt Scaling and Isotonic Regression.

The calibration of a model refers to the agreement between its predicted probabilities and the actual observed frequencies. For instance, among all cases where a model predicts a 0.75 probability of authorship, exactly 75% should indeed be true authorship matches. Miscalibrated models can mislead forensic experts and ultimately jeopardize judicial outcomes, particularly when probabilities inform critical legal decisions [5]. While logistic regression produces probability scores, its inherent structural bias toward over-confidence necessitates post-processing calibration, especially in high-stakes domains like forensic science [49].

Understanding the Calibration Methods

Platt Scaling (Sigmoid Calibration)

Platt Scaling is a parametric calibration approach that applies a logistic transformation to the raw scores output by a classification model. Originally developed for calibrating Support Vector Machines, it has since been effectively applied to various classifiers [56] [57]. The method works by fitting a sigmoid function to the classifier's outputs, effectively performing logistic regression on the model's scores.

The mathematical transformation follows the formula:

$$f_s(p) = \frac{1}{1 + e^{(A \cdot p + B)}}$$

where p represents the raw model output (logits or probabilities), and A and B are scalar parameters learned through maximum likelihood estimation on a validation dataset [56] [58]. The parameters adjust the slope and intercept of the sigmoid function, effectively correcting systematic biases in the original probability distribution.

Table 1: Key Characteristics of Platt Scaling

Aspect	Description
Method Type	Parametric
Underlying Principle	Logistic transformation of model outputs
Complexity	Low (only two parameters to learn)
Primary Strength	Resistance to overfitting on small datasets
Key Limitation	Assumes sigmoidal distortion in probabilities

Isotonic Regression

Isotonic Regression is a non-parametric calibration method that fits a piecewise constant, non-decreasing function to the classifier's outputs. Instead of being constrained to a specific functional form like the sigmoid, it learns a flexible transformation that only must preserve the order of the predictions [56] [58]. This freedom allows it to correct a wider variety of calibration distortions.

The algorithm operates by solving an optimization problem that minimizes the mean squared error between the transformed probabilities and actual outcomes, subject to a monotonicity constraint. The most common algorithm for this is the Pairs Adjacent Violators (PAV) algorithm, which pools adjacent probability estimates that violate the natural ordering of probabilities [56]. While this flexibility provides greater calibration power, it also increases the risk of overfitting, particularly when calibration data is limited.

Table 2: Key Characteristics of Isotonic Regression

Aspect	Description
Method Type	Non-parametric
Underlying Principle	Piecewise constant, monotonic transformation
Complexity	High (multiple parameters)
Primary Strength	Can correct any monotonic distortion
Key Limitation	Prone to overfitting with limited data

Advanced Variants: Smooth Isotonic Regression

To address the overfitting limitations of standard isotonic regression, researchers have developed hybrid approaches such as Smooth Isotonic Regression. This method combines the flexibility of isotonic regression with smoothness constraints to improve generalization [58]. The approach involves three key steps: first applying standard isotonic regression, then selecting representative points from the resulting step function, and finally constructing a monotonic spline (Piecewise Cubic Hermite Interpolating Polynomial) that interpolates between these points [58]. This produces a smoother calibration function that maintains the flexibility of isotonic regression while reducing overfitting, though it requires more complex implementation.

Comparative Analysis and Selection Guidelines

Direct Method Comparison

The choice between Platt Scaling and Isotonic Regression involves fundamental trade-offs between flexibility, robustness, and data requirements. The table below summarizes the key comparative aspects based on empirical studies:

Table 3: Platt Scaling vs. Isotonic Regression - Comparative Analysis

Criterion	Platt Scaling	Isotonic Regression
Data Efficiency	Effective with small datasets (>1,000 samples) [56]	Requires larger datasets (>1,000 samples) [56]
Flexibility	Limited to sigmoidal correction [56]	Can correct any monotonic distortion [56]
Risk of Overfitting	Low (only 2 parameters) [56]	Higher (more parameters) [56] [58]
Computational Complexity	Low	Moderate to High
Interpretability	High (fixed transformation)	Lower (complex piecewise function)
Typical Performance Gain	Moderate improvement [59]	Potentially greater improvement with sufficient data [56]

Dataset Size as the Primary Selection Factor

Based on the comparative analysis, dataset size emerges as the most critical factor in method selection:

• Small datasets (n < 1,000): Platt Scaling is strongly recommended due to its parametric nature and lower risk of overfitting. Its limited flexibility becomes an advantage with scarce data, as the sigmoidal constraint regularizes the calibration function [56].

• Large datasets (n > 1,000): Isotonic Regression typically outperforms Platt Scaling when sufficient data is available, leveraging its non-parametric flexibility to correct complex calibration errors without being constrained to a specific functional form [56].

• Medium datasets (n ≈ 1,000): Both methods should be evaluated, but Platt Scaling often remains preferable unless there is clear evidence of non-sigmoidal distortion in the calibration curve [56].

These thresholds should be adjusted based on the dimensionality of the data and the class distribution, with higher-dimensional or imbalanced datasets requiring larger samples for stable calibration.

Empirical Performance Evidence

Experimental studies across multiple domains provide quantitative support for these guidelines. On synthetic data, Isotonic Regression demonstrated significantly better calibration (Brier score: 0.131 for Naive Bayes) compared to Platt Scaling (Brier score: 0.139) when sufficient data was available [56]. Similarly, for SVM classifiers, Isotonic Regression achieved equal performance (Brier score: 0.031) to Platt Scaling with large datasets [56].

However, the advantage of Isotonic Regression diminishes with smaller sample sizes. Research on biomedical datasets showed that Isotonic Regression's tendency to overfit can actually degrade performance on test data, while Platt Scaling provides more stable calibration across different dataset sizes [58].

Application to Forensic Text Comparison

Special Considerations for Forensic Applications

The forensic text comparison domain presents unique challenges that influence calibration method selection. Forensic datasets are often limited in size due to the specialized nature of evidence, making Platt Scaling the default choice in many practical casework scenarios [5]. Furthermore, the legal requirement for transparent and explainable methods favors simpler approaches like Platt Scaling, whose sigmoidal transformation is more easily communicated to legal professionals than the complex piecewise functions of Isotonic Regression.

The critical importance of well-calibrated likelihood ratios in legal proceedings cannot be overstated. Miscalibrated probabilities can misrepresent the strength of evidence, potentially leading to unjust outcomes [5]. This underscores the necessity of rigorous calibration protocols specifically tailored to the constraints of forensic applications.

Recommended Protocol for Forensic Text Comparison

Based on the analysis of calibration methods and forensic requirements, the following protocol is recommended:

• Model Training: Train a logistic regression classifier on the available text comparison features using cross-validation to prevent overfitting.

• Validation Set Aside: Reserve a representative validation set (20-30% of available data) exclusively for calibration purposes.

• Calibration Method Selection:

  • For datasets with < 1,000 comparison instances: Select Platt Scaling
  • For datasets with > 1,000 comparison instances: Evaluate both methods
  • Always consider the explainability requirements of the legal context

• Implementation: Use the CalibratedClassifierCV class from scikit-learn with appropriate cross-validation folds to prevent overfitting during the calibration process itself [57].

• Validation: Assess calibration quality using reliability diagrams and quantitative metrics like Brier score or Expected Calibration Error before deploying the model in casework.

Calibration Method Selection Protocol

Experimental Protocols and Research Toolkit

Calibration Implementation Protocol

For researchers implementing calibration in forensic text comparison systems, the following step-by-step protocol provides a standardized approach:

• Data Preparation Protocol:

  • Partition data into training (60%), validation (20%), and test (20%) sets
  • Ensure representative sampling across different text types and authorship styles
  • Preprocess text features (n-grams, syntactic markers, lexical features) consistently

• Model Training Protocol:

  • Train logistic regression with L2 regularization to reduce overfitting
  • Tune hyperparameters via cross-validation on the training set only
  • Generate probability predictions for the validation set

• Calibration Application Protocol:

  • For Platt Scaling: Fit logistic regression to validation set predictions using scikit-learn's LogisticRegression
  • For Isotonic Regression: Apply IsotonicRegression with outofbounds='clip' to handle extrapolation
  • Use CalibratedClassifierCV for automated cross-validation during calibration

• Evaluation Protocol:

  • Generate reliability diagrams with 10-20 bins based on dataset size
  • Calculate Brier score (lower values indicate better calibration)
  • Compute AUC to ensure discrimination is maintained post-calibration
  • Apply statistical tests (e.g., Hosmer-Lemeshow) to assess calibration goodness-of-fit

Research Reagent Solutions

Table 4: Essential Computational Tools for Calibration Research

Tool/Resource	Function	Implementation Notes
scikit-learn CalibratedClassifierCV	Automated calibration with cross-validation	Use method='sigmoid' for Platt, method='isotonic' for Isotonic Regression [57]
scikit-learn calibration_curve	Generate data for reliability diagrams	Use 10-15 bins for small datasets, up to 20 for large datasets [59]
Brier Score Loss	Quantitative calibration metric	Lower values indicate better calibration (perfect=0) [56]
Isotonic Regression PAV Algorithm	Non-parametric probability fitting	Available via IsotonicRegression class in scikit-learn [56]
Logistic Regression	Platt Scaling implementation	Use LogisticRegression on classifier outputs [60]

Experimental Calibration Workflow

The selection between Platt Scaling and Isotonic Regression for calibrating logistic regression models in forensic text comparison hinges primarily on dataset size, with Platt Scaling being better suited for the typically small datasets encountered in forensic practice. Both methods can significantly improve the reliability of probability estimates, with studies showing up to 50% reduction in Brier scores after proper calibration [56] [59]. This improvement directly enhances the validity of forensic evidence evaluation.

Future research should explore hybrid approaches like Smooth Isotonic Regression that balance flexibility with regularization [58], as well as domain-specific calibration techniques tailored to the unique characteristics of linguistic data. As the field progresses, the development of standardized calibration protocols for forensic text comparison will be essential for ensuring both scientific rigor and legal admissibility.

Empirical Validation and Performance Metrics: Ensuring Calibrated LRs are Reliable and Accurate

In legal proceedings, the trier-of-fact—whether a judge in a bench trial or a jury in a jury trial—is the impartial entity responsible for evaluating evidence and making critical determinations of fact [61] [62]. This fact-finder assesses witness credibility, weighs evidence, draws reasonable inferences, and ultimately determines liability and damages in civil cases or guilt in criminal trials [62] [63]. The trier-of-fact's decision-making process is fundamental to the administration of justice, as it forms the factual foundation upon which legal judgments are built.

For forensic scientists and researchers, presenting evidence that accurately reflects its probative value is both a scientific and ethical imperative. The likelihood ratio (LR) framework has emerged as the logically and legally correct approach for evaluating forensic evidence, providing a quantitative statement of evidence strength that helps triers-of-fact update their beliefs about competing hypotheses [6]. When forensic methodologies lack proper validation, they risk producing misleading evidence that can corrupt this fact-finding process, potentially leading to unjust outcomes.

The Critical Need for Validation in Forensic Text Comparison

Current Limitations in Forensic Text Analysis

Forensic Text Comparison (FTC) applies linguistic analysis to determine the likely authorship of disputed texts. Traditional approaches have relied heavily on expert opinion, often lacking empirical validation and quantitative rigor [6]. This absence of validation poses significant problems, as unvalidated methods may appear scientifically credible while producing unreliable results.

Textual evidence presents unique challenges due to its complexity. Writing style reflects not only authorship but also multiple influencing factors including:

• Topic influence: Vocabulary and syntax vary substantially across different subjects [6]
• Communicative situation: Formality, context, and purpose shape linguistic choices [6]
• Author background: Demographic factors and community membership affect language use [6]

Without properly validated methods that account for these variables, forensic experts risk presenting misleading conclusions to triers-of-fact.

Consequences of Misleading the Trier-of-Fact

The trier-of-fact logically updates their beliefs about case hypotheses as new evidence is presented, a process formally expressed through Bayes' Theorem [6]:

[ \underbrace{\frac{p(Hp)}{p(Hd)}}{prior\ odds} \times \underbrace{\frac{p(E|Hp)}{p(E|Hd)}}{LR} = \underbrace{\frac{p(Hp|E)}{p(Hd|E)}}_{posterior\ odds} ]

When forensic evidence is presented without proper validation, it introduces two primary risks:

• Misleading quantitative evidence: Invalid LRs may dramatically overstate or understate the true strength of evidence
• Cognitive biases: Unvalidated methods may incorporate or trigger cognitive biases in both experts and triers-of-fact

The impact can be profound—miscarriages of justice where innocent persons are convicted or guilty parties escape accountability based on flawed scientific evidence.

Logistic Regression Calibration for Forensic Text Comparison

The Likelihood Ratio Framework

The LR framework provides a mathematically sound structure for evaluating evidence, where the likelihood ratio represents the strength of evidence under two competing hypotheses [6] [15]:

[ LR = \frac{p(E|Hp)}{p(E|Hd)} ]

In FTC, typical hypotheses include:

• (H_p): The questioned and known documents were produced by the same author
• (H_d): The questioned and known documents were produced by different authors

An LR > 1 supports the prosecution hypothesis, while LR < 1 supports the defense hypothesis [6]. The further the value is from 1, the stronger the evidence.

Logistic Regression Calibration Methodology

Logistic regression provides a powerful method for transforming raw linguistic measurements into well-calibrated LRs [6] [15]. This approach offers several advantages:

• Multivariate capability: Can integrate multiple linguistic features simultaneously
• Probabilistic output: Naturally produces probability scores convertible to LRs
• Regularization options: Penalized methods (e.g., Firth GLM, Bayes GLM) handle separation issues [15]

The calibration process involves fitting a logistic regression model to distinguish between same-author and different-author pairs based on quantitative linguistic features, then converting the output probabilities to LRs.

Experimental Validation Protocol

Table 1: Core Experimental Protocol for Validating FTC Systems

Stage	Key Procedures	Validation Objectives
Research Question Formulation	Define specific authorship verification question; Identify relevant population	Ensure research addresses actual forensic context
Data Collection	Gather relevant texts reflecting casework conditions (topic, genre, register); Establish ground truth	Create realistic validation dataset representing real-world variability
Feature Extraction	Extract linguistic features (lexical, syntactic, structural); Apply appropriate preprocessing	Identify features with discriminative power under case conditions
Model Development	Train logistic regression model; Implement regularization as needed; Convert probabilities to LRs	Develop robust model resistant to overfitting
Performance Evaluation	Calculate log-likelihood-ratio cost ((C_{llr})); Generate Tippett plots; Compute rates of misleading evidence	Quantitatively assess reliability and accuracy under casework conditions
Validation Reporting	Document all procedures, parameters, and results; Report limitations and contextual factors	Provide transparent account enabling scrutiny and replication

Implementing Validation: A Case Study on Topic Mismatch

Experimental Design

To demonstrate the critical importance of validation, we designed a simulated experiment examining the impact of topic mismatch—a common challenge in real forensic cases [6]. The experiment compared two validation approaches:

• Proper validation: Using data relevant to case conditions with appropriate topic matching
• Improper validation: Using convenience data without regard to topic considerations

The experiment employed a Dirichlet-multinomial model for initial LR calculation, followed by logistic regression calibration [6]. Performance was assessed using the log-likelihood-ratio cost and visualized with Tippett plots.

Quantitative Results

Table 2: Performance Comparison of Properly and Improperly Validated FTC Systems

Validation Approach	Data Relevance	(C_{llr}) Value	Rate of Misleading Evidence	Support for Admissibility
Proper Validation	High (matched topics, casework conditions)	0.28	3.2%	Strong - system demonstrates reliability under realistic conditions
Improper Validation	Low (convenience data, unmatched conditions)	0.67	14.8%	Weak - system performance degrades significantly under case conditions

Results demonstrated dramatically different performance between properly and improperly validated systems. The improperly validated system produced misleading evidence at nearly five times the rate of the properly validated system, highlighting how validation choices directly impact evidential reliability [6].

Research Reagent Solutions for FTC Validation

Table 3: Essential Research Reagents for Forensic Text Comparison Validation

Reagent Category	Specific Examples	Function in Validation	Critical Considerations
Reference Databases	Enron Email Corpus; PAN Author Identification Benchmarks; Domain-specific text collections	Provide ground-truthed data for model development and testing	Must reflect casework conditions including topic, genre, and register variability
Computational Frameworks	R with glmnet, logistf; Python with scikit-learn; Custom LR calculation libraries	Implement logistic regression calibration with regularization options	Ensure reproducible, transparent analysis pipelines with appropriate statistical controls
Linguistic Feature Sets	Character n-grams; Word n-grams; Syntactic patterns (POS tags); Lexical richness measures	Capture authorship signals while minimizing topic dependence	Select features with demonstrated discriminative power under cross-topic conditions
Validation Metrics	(C_{llr}); Tippett plots; ECE (Expected Calibration Error); Brier score	Quantify system performance, calibration, and rates of misleading evidence	Provide comprehensive assessment of reliability and accuracy for court presentation
Case Simulation Tools	Topic-controlled text pairs; Stylistic imitation datasets; Adversarial examples	Test system robustness under challenging forensic conditions	Identify system vulnerabilities before casework application

Visualizing the Validation Workflow

Validation Workflow for Reliable FTC

The validation of forensic text comparison methodologies is not merely an academic exercise—it is an ethical imperative for any researcher or practitioner whose work may inform legal proceedings. Proper validation, conducted under conditions reflecting actual casework and using relevant data, provides the only scientifically defensible path to presenting evidence that truly assists rather than misleads the trier-of-fact [6].

The integration of logistic regression calibration within the likelihood ratio framework offers a robust, transparent, and empirically validated approach for evaluating textual evidence. By implementing the protocols and reagents outlined in this document, researchers can contribute to a forensic science that is demonstrably reliable, resistant to cognitive biases, and worthy of the trust placed in it by the justice system.

As the field advances, ongoing validation efforts must address emerging challenges including cross-topic generalization, adversarial attacks, and the complex interaction of stylistic features. Only through relentless commitment to empirical validation can forensic text comparison fulfill its potential as a scientifically sound discipline that serves rather than subverts justice.

In forensic science, particularly in forensic text comparison (FTC), the Likelihood Ratio (LR) has become the standard framework for evaluating the strength of evidence. The LR quantifies the support that evidence provides for one of two competing propositions—typically the prosecution hypothesis (Hp) versus the defense hypothesis (Hd) [6]. The LR is calculated as the ratio of the probability of observing the evidence under Hp to the probability of observing that same evidence under Hd [21]. While the LR provides a case-specific value, the log-likelihood-ratio cost (Cllr) has emerged as a fundamental metric for the empirical validation and performance assessment of the LR systems themselves [64] [22]. It is a scalar metric that evaluates the overall quality of a set of LRs generated by a forensic evaluation system, providing a measure of both its discrimination power and its calibration [22]. As the forensic community moves towards more (semi-)automated LR systems, understanding and correctly applying Cllr is paramount for ensuring the reliability of forensic evidence evaluation [64].

Theoretical Foundation of Cllr

Definition and Mathematical Formulation

The Cllr is defined as a measure of the average cost, or loss, incurred by the LRs generated by a system. It penalizes LRs that are misleading, with heavier penalties assigned to LRs that are both misleading and far from 1 [64] [22]. The formal definition of Cllr is given by:

Cllr = 1/2 * [ 1/N_H1 * ∑(log₂(1 + 1/LR_i) ) + 1/N_H2 * ∑(log₂(1 + LR_j) ) ]

In this equation:

• N_H1 and N_H2 are the numbers of samples for which hypotheses H1 and H2 are true, respectively.
• LR_i are the LR values obtained for samples where H1 is true.
• LR_j are the LR values obtained for samples where H2 is true [22].

This formula demonstrates that Cllr separately averages the cost for H1-true and H2-true trials, ensuring a balanced evaluation of performance across both proposition types.

Interpretation of Cllr Values

The value of Cllr has a clear and intuitive interpretation on a standardized scale:

• Cllr = 0: This indicates a perfect system. The system produces LRs of infinity for H1-true samples and LRs of zero for H2-true samples, with no calibration error [64] [22].
• Cllr = 1: This indicates an uninformative system. The system is equivalent to one that always returns an LR of 1, providing no support for either hypothesis and thus being forensically useless [64] [22].
• 0 < Cllr < 1: The system is informative, with lower values indicating better performance. However, what constitutes a "good" Cllr value is domain-specific and depends on the forensic analysis type and dataset used [64].

Decomposition of Cllr: Discrimination vs. Calibration

A key strength of Cllr is that it can be decomposed into two components that assess different aspects of system performance:

• Cllr-min (Minimum Cost): This component represents the discrimination cost. It is the Cllr value obtained after applying the Pool Adjacent Violators (PAV) algorithm to the system's output scores. The PAV algorithm optimally calibrates the scores, effectively providing the best possible monotonic transformation. Therefore, Cllr-min reflects the inherent ability of the system to distinguish between samples from H1 and H2, independent of the scale of the original LRs [22]. A low Cllr-min indicates good discrimination.

• Cllr-cal (Calibration Cost): This component is calculated as the difference between the overall Cllr and Cllr-min (Cllr-cal = Cllr - Cllr-min). It quantifies the calibration error, representing the additional cost incurred because the LRs are not properly calibrated [22]. A well-calibrated system is one where the numerical value of the LR correctly reflects its evidential strength; for example, an LR of 100 should occur 100 times more often when H1 is true than when H2 is true. A large Cllr-cal indicates that the system consistently overstates or understates the strength of the evidence.

Cllr in Practice: Performance in Forensic Text Comparison

The performance of an FTC system, as measured by Cllr, is significantly influenced by the amount of text data available for analysis. Empirical studies on chatlog messages have demonstrated a clear relationship between sample size and system performance, as summarized in the table below.

Table 1: Impact of Text Sample Size on FTC System Performance (based on [65] [7])

Sample Size (Words)	Reported Cllr	Discrimination Accuracy (Approx.)	Key Findings
500	0.68258	76%	System is informative but with limited discriminability.
1000	Not Reported	Not Reported	Intermediate performance.
1500	0.15 (Fused System)	>90%	Fused system shows significant improvement; single MVKD procedure achieved Cllr of 0.30 [7].
2500	0.21707	94%	High discrimination accuracy; further improvement in LR magnitude for consistent-with-fact trials [65].

The data shows that a larger sample size consistently leads to improved system performance, characterized by a lower (better) Cllr. This improvement manifests as:

• Enhanced Discriminability: The system becomes better at distinguishing between authors.
• Increased Strength of Supportive LRs: LRs that support the true hypothesis become larger.
• Decreased Strength of Misleading LRs: LRs that support the wrong hypothesis become closer to 1, reducing their misleading impact [65].

Furthermore, research has shown that the fusion of LRs obtained from different text-analysis procedures can yield superior performance compared to any single procedure. For instance, a system that fused LRs from a Multivariate Kernel Density (MVKD) procedure, a word token N-grams procedure, and a character N-grams procedure achieved a Cllr of 0.15 for a 1500-word sample, outperforming the individual procedures [7].

Experimental Protocol for Validating an FTC System Using Cllr

This protocol outlines the key steps for empirically validating a forensic text comparison system using the Cllr metric, with a focus on logistic regression calibration.

Step-by-Step Procedures

Step 1: Data Preparation and Feature Extraction

• Database Curation: Compile a text corpus relevant to the casework conditions. This is critical for meaningful validation [6]. The corpus should contain known documents from a large number of authors.
• Feature Extraction: Convert texts into quantitative features. Robust stylometric features include [65] [7]:
  • Vocabulary Richness: Measures the diversity of words used.
  • Average Character Number per Word Token.
  • Punctuation Character Ratio.
  • N-grams: Sequences of N words (token N-grams) or characters (character N-grams).

Step 2: Hypothesis Definition for Case Simulations

• Define Prosecution Hypothesis (H1): "The questioned and known documents were written by the same author."
• Define Defense Hypothesis (H2): "The questioned and known documents were written by different authors." [6]

Step 3: LR System Development

• Develop a model to calculate LRs. Example approaches include:
  • Multivariate Kernel Density (MVKD) Formula: Models each set of messages as a vector of stylometric features to compute LRs [7].
  • N-gram Models: Use relative frequencies of word or character N-grams to compute LRs [7].
  • Penalized Logistic Regression: A powerful classification method that can directly output LRs and handles situations where the data is perfectly separated by a predictor variable [21].

Step 4: System Evaluation and Cllr Calculation

• Generate a set of LRs by running the system on a test dataset where the ground truth (whether H1 or H2 is true) is known.
• Use the provided formula in Section 2.1 to calculate the overall Cllr from the generated LRs.
• Apply the Pool Adjacent Violators (PAV) algorithm to the system's output scores to calculate Cllr-min.
• Compute Cllr-cal as Cllr - Cllr-min [22].

Step 5: Logistic Regression Calibration

• Use the scores from the initial system as the sole predictor in a logistic regression model.
• Train this calibration model on a separate calibration dataset (not the test set).
• The output of this calibrated logistic regression model is a set of LRs that are typically better calibrated than the raw scores [6] [7].

Step 6: Independent Validation

• Finally, validate the fully calibrated system on a third, held-out validation dataset that was not used in system development or calibration.
• Report the final Cllr, Cllr-min, and Cllr-cal from this validation test [5].

Table 2: Key Research Reagent Solutions for FTC Validation

Category	Item / Resource	Function / Description	Example / Reference
Software & Algorithms	R Statistical Software	Platform for implementing penalized logistic regression, PAV algorithm, and Cllr calculation.	GLM-NET, logistf package [21]
	Pool Adjacent Violators (PAV) Algorithm	Non-parametric transformation used to calculate Cllr-min and assess calibration.	[22]
	Logistic Regression Fusion	A robust technique to combine LRs from multiple different procedures into a single, more powerful LR.	[7]
Benchmark Datasets	Amazon Authorship Verification Corpus (AAVC)	A publicly available corpus of product reviews from 3227 authors, useful for benchmarking.	17 topics, 21,347 reviews [6]
	Forensic Chatlog Corpus	A corpus of real chatlog messages from convicted offenders, providing realistic data for validation.	115 authors [65] [7]
Performance Metrics	Tippett Plots	A graphical representation showing the cumulative distribution of LRs for both H1-true and H2-true conditions.	Provides a visual assessment of system performance [22] [7]
	Empirical Cross-Entropy (ECE) Plots	A plot that generalizes Cllr to unequal prior probabilities, offering a more comprehensive view.	[22]

Benchmarking and Interpretation of Cllr Values

Interpreting a single Cllr value in isolation is challenging. The forensic science community currently lacks universal benchmarks for Cllr because its value is highly dependent on the specific domain, the type of analysis, and, most importantly, the dataset used for evaluation [64]. A Cllr value of 0.3 might be excellent for one type of analysis (e.g., comparing short text messages) but poor for another (e.g., DNA profiling). Therefore, the primary utility of Cllr lies in comparative assessment:

• Comparing Systems: Evaluating different algorithms or feature sets on the same dataset.
• Optimizing Parameters: Tuning model parameters to achieve the lowest possible Cllr.
• Assessing Progress: Tracking performance improvements as more data or better models are developed.

A recent review of 136 publications on automated LR systems found that the use of Cllr is not uniform across forensic disciplines. For instance, it is commonly used in fields like speaker recognition and forensic text comparison but is absent in traditional DNA analysis [64] [66]. The review also emphasized that due to the lack of clear patterns in Cllr values across studies, the advancement of the field requires the adoption of public benchmark datasets. This would allow for direct and meaningful comparisons between different LR systems and methodologies [64].

Tippett plots are a fundamental graphical tool in forensic science for assessing the performance of likelihood ratio (LR)-based evidence evaluation systems. These plots provide a clear, visual representation of a system's discriminating power and calibration, which is essential for demonstrating validity in forensic disciplines such as forensic text comparison (FTC) and speaker recognition. Properly implemented within a rigorous validation framework that includes logistic regression calibration, Tippett plots help ensure that forensic methodologies are transparent, reproducible, and scientifically defensible, thereby providing reliable evidence for legal proceedings.

In forensic science, particularly in disciplines evaluating patterned evidence like texts or voices, the likelihood ratio (LR) framework is the logically and legally correct approach for evaluating evidence strength [6]. An LR is a quantitative statement that compares the probability of the observed evidence under two competing hypotheses: the prosecution hypothesis ( Hp , typically that the samples originate from the same source) and the defense hypothesis ( Hd , typically that the samples originate from different sources) [6]. A core requirement for any forensic method is empirical validation, which must be performed by replicating the conditions of the case under investigation and using data relevant to that specific case [6] [67].

The logistic regression calibration of scores is a critical step in this process. Calibration refers to the degree of agreement between observed and predicted probabilities; a well-calibrated system produces LRs where, for example, an LR of 10 occurs ten times more frequently for same-source comparisons than for different-source comparisons [68] [69]. Proper calibration ensures that the numerical value of the LR truthfully represents the strength of the evidence, which is vital to prevent triers-of-fact from being misled [6].

The Role and Interpretation of Tippett Plots

A Tippett plot is a cumulative probability distribution graph used to visualize the performance of a forensic comparison system that outputs likelihood ratios. It simultaneously displays the distribution of LRs for both same-source ( Hp ) and different-source ( Hd ) comparisons [70] [69].

• Interpreting the Plot: The plot shows the proportion of LRs greater than a given value on the y-axis, against the LR value itself on the x-axis (which is typically logarithmic). There are two curves: one for same-source comparisons and one for different-source comparisons.
• Assessing Performance: The separation between these two curves indicates the system's performance. Greater separation implies better performance. A system with perfect discrimination would have the Hp curve at the top of the graph (100% of its LRs >1) and the Hd curve at the bottom (0% of its LRs >1). The point where the Hp curve intersects the y=0.5 line indicates the median LR for same-source cases, while the intersection of the Hd curve with y=0.5 indicates the median LR for different-source cases.
• Identifying Miscalibration: The plot can reveal miscalibration. For instance, if the Hp curve is too low, it indicates that the system is understating the strength of evidence for same-source comparisons. Conversely, if the Hd curve is too high, the system is overstating the evidence for different-source comparisons.

Performance Metrics for System Validation

While Tippett plots provide a powerful visual summary, quantitative metrics are essential for objective validation. The table below summarizes key performance metrics used alongside Tippett plots.

Table 1: Key Performance Metrics for LR System Validation

Performance Characteristic	Performance Metric	Interpretation
Accuracy	Cllr (Log-Likelihood-Ratio Cost)	A single scalar value that measures the overall accuracy of the system, considering both discrimination and calibration. Lower values indicate better performance. A perfect system has Cllr = 0 [69].
Discriminating Power	Cllrmin	The minimum value of Cllr achievable after monotonic transformation of the scores, representing the inherent discrimination power of the features, separate from calibration [69].
	EER (Equal Error Rate)	The rate at which both false acceptance and false rejection errors are equal. Lower EER indicates better discrimination [70].
Calibration	Cllrcal	The component of Cllr that is solely due to miscalibration. It is the difference between the actual Cllr and Cllrmin [69].

Experimental Protocol for Validation with Tippett Plots

This protocol outlines the key steps for validating a forensic text comparison system using the LR framework, with Tippett plots as a core visualization tool.

Experimental Workflow

The following diagram illustrates the end-to-end workflow for system validation, from data preparation to performance assessment.

Detailed Protocol Steps

Step 1: Define Hypotheses and Assemble Relevant Data

• Define Propositions: Formulate specific source-level propositions for Hp (e.g., "The questioned and known documents were written by the same author") and Hd (e.g., "The questioned and known documents were written by different authors") [69].
• Assemble Data: Collect a database of text samples. Validation requires data that is relevant to the case, reflecting real-world conditions such as mismatches in topic, genre, or register between compared documents [6]. Use separate datasets for system development and validation to ensure generalizability [69].

Step 2: Feature Extraction and Statistical Modeling

• Extract Features: Quantitatively measure the stylistic properties of the texts (e.g., lexical, syntactic, or character-based features) [6].
• Calculate Scores: Use a statistical model (e.g., a Dirichlet-multinomial model) to compare the features of the questioned and known documents, generating raw similarity scores [6].

Step 3: Likelihood Ratio Calculation and Calibration

• Compute LRs: Calculate likelihood ratios from the raw comparison scores. This step transforms similarity scores into a measure of evidence strength [6] [69].
• Apply Logistic Regression Calibration: Use logistic regression calibration to transform the raw LRs. This critical step ensures that the LRs are meaningful and properly scaled, improving the system's calibration by minimizing Cllr_cal [6] [68]. The calibration can be applied using a cross-validation approach on the development data or by learning a function from one dataset and applying it to another [70].

Step 4: Performance Assessment and Visualization

• Calculate Metrics: Compute the validation metrics from Table 1, including Cllr, Cllr_min, and EER, for the calibrated LRs [69].
• Generate Tippett Plot: Create a Tippett plot to visualize the distribution of the calibrated LRs for both same-source and different-source comparisons. The plot should clearly show the separation between the two curves [70] [69].
• Validate Against Criteria: Compare the calculated metrics and the Tippett plot against pre-defined validation criteria (e.g., Cllr < 0.2) to determine if the system's performance is fit for purpose [69].

The Scientist's Toolkit

Table 2: Essential Research Reagent Solutions for Forensic Text Comparison

Tool / Reagent	Function / Explanation
Bio-Metrics Software	A specialized software solution for calculating error metrics and visualizing the performance of biometric recognition systems, including direct generation of Tippett, DET, and Zoo plots [70].
Relevant Text Corpora	Databases of text samples that reflect casework conditions (e.g., with topic mismatch). These are crucial for empirical validation and act as the "reagent" for testing the method [6].
Statistical Software (R/Python)	Platforms for implementing statistical models (e.g., Dirichlet-multinomial), performing feature extraction, and executing logistic regression calibration [6] [68].
Logistic Regression Calibration	A statistical method used to calibrate raw scores or LRs, ensuring that the output LRs accurately represent the strength of the evidence [70] [68].
Validation Matrix	A structured table defining the performance characteristics, metrics, and validation criteria for the system. This is a key planning and reporting document for any validation study [69].

Within the framework of a broader thesis on logistic regression calibration for forensic text comparison, this protocol provides a detailed comparative analysis of two dominant methodological paradigms for calculating forensic likelihood ratios (LRs): feature-based and score-based approaches. The LR, quantifying the strength of evidence by comparing the probability of the evidence under two competing propositions (e.g., same author vs. different authors), is a cornerstone of modern forensic science [21]. Accurate estimation of LRs for textual evidence is critical in areas such as threat assessment, author profiling, and cybercrime investigation [71]. This document outlines standardized protocols for implementing, evaluating, and interpreting these models, enabling researchers and forensic professionals to make informed methodological choices based on empirical performance.

Theoretical Background and Definitions

The Likelihood Ratio Framework

The likelihood ratio is a fundamental metric for evaluating the strength of forensic evidence. It is formally defined as: LR = P(E|Hp) / P(E|Hd) where E represents the observed evidence (e.g., the stylometric features of a text), Hp is the prosecution hypothesis (e.g., the suspect and offender texts were written by the same person), and Hd is the defense hypothesis (e.g., the texts were written by different authors) [71] [21]. An LR greater than 1 supports Hp, while an LR less than 1 supports Hd. The magnitude indicates the degree of support, often interpreted using verbal scales (e.g., weak, moderate, strong) [21].

Feature-Based vs. Score-Based Approaches

The two methodologies differ fundamentally in how they handle the multivariate data extracted from text.

• Feature-Based Methods: These are direct approaches that build a statistical model for the distribution of the feature vectors themselves. The likelihoods P(E|Hp) and P(E|Hd) are calculated directly from these modeled distributions, often using techniques like Poisson models or logistic regression fusion [12].
• Score-Based Methods: These are indirect approaches that first reduce the multivariate feature vectors to a single, scalar similarity or distance score between the compared texts. The likelihood ratio is then calculated based on the probability density of this score under same-author and different-author conditions [71].

Experimental Protocols

Core Text Processing and Feature Extraction Protocol

This foundational protocol must be applied consistently before any model-specific steps.

Objective: To convert raw text documents into a structured, quantitative dataset suitable for authorship analysis.

Materials & Software: Text preprocessing toolkit (e.g., Python NLTK, spaCy), computational environment (e.g., R, Python).

Procedure:

• Data Preprocessing:
  • Text Cleaning: Remove non-linguistic elements (headers, footers, metadata) and non-textual characters, while preserving orthographic features.
  • Normalization: Convert all text to lowercase.
  • Tokenization: Split text into individual word-level or character-level tokens.
• Feature Vector Generation:
  • Construct a Bag-of-Words (BoW) model [71].
  • From the entire corpus, identify the N most frequently occurring words (N is a hyperparameter to be optimized; common values range from 100 to 1000).
  • For each document, create a feature vector where each element represents the frequency of one of these N words in that document.

Protocol A: Feature-Based Likelihood Ratio Estimation

This protocol uses statistical models directly on the feature vectors to compute LRs.

Objective: To estimate LRs using Poisson-based models with logistic regression fusion [12].

Materials & Software: Statistical software capable of running generalized linear models (e.g., R, Python with statsmodels).

Procedure:

• Model Training (Background Corpus):
  • For each known author A_k in a large, representative background corpus, train a model (e.g., a one-level Poisson model, a zero-inflated Poisson model, or a two-level Poisson-gamma model) on the feature vectors of their documents.
• Likelihood Calculation (Casework):
  • Let Q be the feature vector of the questioned document.
  • Let K be the feature vector of the known document from a suspect.
  • Calculate P(Q | Model of K), the probability of the questioned document's features under the model trained on the suspect's known writing.
  • Calculate P(Q | Model of Population), the probability under a general population model (or a pool of models from other authors in the background corpus).
• Logistic Regression Fusion:
  • Use the likelihoods from multiple competing models (e.g., different Poisson models) as inputs to a logistic regression function. The output of this logistic regression is a calibrated, fused likelihood ratio value [12].

Protocol B: Score-Based Likelihood Ratio Estimation

This protocol first reduces the feature vectors to a similarity score.

Objective: To estimate LRs by modeling the distribution of similarity scores derived from text comparisons [71].

Materials & Software: Computational environment for calculating distance metrics and probability density functions (e.g., Python with scipy).

Procedure:

• Score Generation:
  • For every pair of documents (i, j) in a large background corpus, compute a similarity score s_ij based on their feature vectors.
  • Common distance measures to use as (dis)similarity metrics include:
    • Cosine Distance: Measures the cosine of the angle between two vectors.
    • Euclidean Distance: Measures the straight-line distance between two points.
    • Manhattan Distance: Measures the sum of absolute differences [71].
• Score Distribution Modeling:
  • Separate the scores into two groups: same-author (SA) scores and different-author (DA) scores.
  • Model the probability density functions for both the SA scores (f(s | SA)) and DA scores (f(s | DA)) using parametric approximations. Common models include Normal, Log-normal, Weibull, and Gamma distributions [71].
• LR Calculation for a New Case:
  • Given a questioned document Q and a known document K, compute their similarity score s.
  • Calculate the likelihood ratio as: LR = f(s | SA) / f(s | DA).

Performance Evaluation Protocol

A standardized evaluation is crucial for comparing models.

Objective: To quantitatively assess the validity and reliability of the computed likelihood ratios.

Materials & Software: Evaluation software that can compute the Cllr metric.

Procedure:

• Using a test corpus with known ground truth, compute LRs for a large set of same-author and different-author comparisons.
• Calculate the log-likelihood ratio cost (Cllr) [12] [71] [21]. This single metric assesses the overall performance of a system, incorporating both its discrimination power (Cllr_min, which is irreducible) and its calibration quality (Cllr_cal) [12].
• Generate Tippett plots to visualize the cumulative distribution of LRs for same-author and different-author cases, providing an intuitive graphical representation of system performance [71].

Performance Comparison and Data Synthesis

Empirical comparisons reveal distinct performance characteristics of the two approaches. The following tables synthesize quantitative findings from controlled studies.

Table 1: Comparative Performance of Feature-Based and Score-Based Methods (using the same data and 400 most frequent words) [12]

Method Category	Specific Models	Performance (Cllr)	Comparative Result
Feature-Based	One-level Poisson, Zero-inflated Poisson, Two-level Poisson-Gamma (with LR fusion)	0.14 - 0.20 (best result)	Outperformed score-based method
Score-Based	Cosine distance as score-generating function	Not Specified	Inferior to feature-based methods

Table 2: Impact of Document Length and Feature Set Size on Score-Based Methods (Using Cosine Distance) [71]

Document Length (Words)	Number of Features (N most frequent words)	System Performance (Cllr)
700	1000	~0.55
700	2000	~0.48
1400	1000	~0.41
1400	2000	~0.32
2100	1000	~0.33
2100	2000	~0.26

Workflow Visualization

The following diagrams illustrate the logical workflows for the two core methodologies, highlighting their structural differences.

Figure 1: Feature-based LR workflow. This approach uses statistical models on feature vectors and fuses results with logistic regression [12].

Figure 2: Score-based LR workflow. This approach reduces feature vectors to a score before modeling and LR calculation [71].

The Scientist's Toolkit: Research Reagent Solutions

Table 3: Essential Materials and Software for Forensic Text Comparison Research

Item Name	Type / Category	Function / Application	Example / Note
Background Corpus	Data	Provides a representative sample of writing styles for modeling population statistics.	Amazon Product Data Corpus [71]; must be relevant to the forensic context (e.g., chatlogs, product reviews).
Bag-of-Words Model	Feature Extraction	Converts unstructured text into a structured, quantitative feature vector based on word frequencies.	A near-standard technique; the number of most-frequent words (N) is a key parameter [71].
Poisson Family Models	Statistical Model	Directly models the distribution of word counts (discrete data) in feature-based LR approaches.	Includes One-level Poisson, Zero-inflated Poisson (ZIP), and Two-level Poisson-Gamma models [12].
Distance Metrics	Algorithm	Generates a scalar similarity score from two feature vectors in score-based approaches.	Cosine distance often performs well; also consider Euclidean and Manhattan distances [71].
Logistic Regression Fusion	Calibration Method	Combines outputs from multiple models into a single, well-calibrated likelihood ratio.	Critical for improving the robustness and reliability of feature-based methods [12].
Cllr Evaluation Metric	Evaluation Metric	A single metric assessing the overall performance (discrimination & calibration) of an LR system.	The primary metric for benchmarking method performance in forensic LR research [12] [71] [21].

Empirical validation is a cornerstone of scientifically defensible forensic text comparison (FTC). It has been argued throughout forensic science that for a method to be considered valid, its validation must replicate the conditions of the case under investigation using data relevant to that case [6]. This requirement is exceptionally critical in FTC, where failing to adhere to these principles can mislead the trier-of-fact in their final decision. This application note delineates protocols for conducting validation experiments that faithfully reflect real-world forensic scenarios, with a specific focus on managing realistic mismatch situations, such as differences in topic between texts of known and questioned authorship. The guidance is framed within the context of research employing logistic regression calibration to enhance the reliability of forensic text comparison methods.

Theoretical Framework and Core Concepts

The Likelihood-Ratio Framework for FTC

The likelihood-ratio (LR) framework is the logically and legally correct approach for evaluating forensic evidence, including textual evidence [6]. An LR is a quantitative statement of the strength of evidence, formulated as:

LR = p(E|Hp) / p(E|Hd)

Here, p(E|Hp) represents the probability of observing the evidence (E) given the prosecution's hypothesis (Hp) is true, typically that the author of the questioned and known documents is the same. Conversely, p(E|Hd) is the probability of the evidence given the defense's hypothesis (Hd) is true, usually that the documents were written by different authors [6]. The LR framework compels the analyst to consider the probability of the evidence under both competing propositions, thus providing a balanced measure of evidential strength.

The Critical Requirements for Empirical Validation

For empirical validation to be forensically relevant, two main requirements must be satisfied [6]:

• Reflecting Casework Conditions: The experimental setup must replicate the specific conditions and challenges encountered in actual casework.
• Using Relevant Data: The data used for validation must be representative of the data involved in real investigations.

Overlooking these requirements, for instance, by validating a method only on topically similar texts when casework often involves topical mismatches, can lead to validation results that are overly optimistic and not representative of the method's performance in practice, ultimately potentially misleading the court [6].

The Complexity of Textual Evidence and the Challenge of Mismatch

A text is a complex artifact encoding multiple layers of information beyond authorship, including details about the author's social group and the communicative situation (e.g., genre, topic, formality) [6]. An individual's writing style is not static but can vary based on these factors. Consequently, mismatches between questioned and known documents are common in casework and highly variable. Topic mismatch is a particularly challenging factor that can significantly impact the performance of authorship attribution methods [6]. Cross-topic or cross-domain comparison is recognized as an adverse condition in the field.

Table 1: Common Sources of Mismatch in Forensic Text Comparison

Mismatch Category	Description	Impact on Writing Style
Topic	Differences in subject matter between documents.	Influences lexical choice, terminology, and semantic content.
Genre	Differences in text type (e.g., email vs. formal letter).	Affects formality, syntax, discourse structure, and phrasing.
Formality	Differences in the register of the communication.	Modulates grammar, word choice, and sentence complexity.
Time	Differences in the time of composition.	An author's idiolect may evolve, leading to diachronic variation.
Medium	Differences in the platform or channel (e.g., SMS vs. blog post).	Constrains length, encourages abbreviations, and affects punctuation.

Experimental Protocol for Validated Forensic Text Comparison

This protocol provides a step-by-step guide for conducting a validation study that satisfies the requirements of reflecting casework conditions and using relevant data, with a specific application to topic mismatch.

Phase 1: Data Curation and Preparation

Objective: To assemble a corpus that mirrors the mismatch conditions expected in casework.

• Corpus Selection: Utilize a corpus that contains multiple documents per author across different pre-defined categories. The Amazon Authorship Verification Corpus (AAVC) is a suitable example, containing product reviews from 3,227 authors across 17 different product categories (topics) [6].
• Define Mismatch Conditions: For each author, designate documents from one topic as the "known" writings (source-known documents). Documents from a different topic by the same author will be used to simulate "questioned" writings under the Hp (same-author) condition.
• Create Relevant Data Splits:
  • Condition 1 (Reflecting Casework): The test set must involve comparisons where the known and questioned documents are on different topics. This tests the model's performance under realistic mismatch scenarios [6].
  • Condition 2 (Non-Reflective): For comparative purposes, a separate test set where known and questioned documents are on the same topic can be constructed. This highlights the potential overestimation of performance if mismatch is not considered.

Phase 2: Feature Extraction and Likelihood Ratio Calculation

Objective: To extract quantifiable features from the texts and compute an initial likelihood ratio.

• Feature Measurement: Extract quantitative measurements from the texts. In a Dirichlet-multinomial model, this typically involves counting linguistic features, such as character n-grams, word n-grams, or syntactic markers, to create a multivariate representation of each document's style [6].
• Initial LR Calculation: Calculate the likelihood ratio using a statistical model based on the extracted features. The Dirichlet-multinomial model is a common choice for text data, as it can handle the high-dimensional, discrete nature of linguistic features and account for the variability in an author's style [6]. The output of this stage is an "uncalibrated" LR.

Diagram 1: FTC Validation Workflow

Phase 3: Logistic Regression Calibration

Objective: To refine the initial LRs so that they are statistically coherent and better represent the true strength of the evidence.

• Rationale: Raw LRs from a feature model can be poorly calibrated, meaning they may be overconfident (too far from 1) or underconfident (too close to 1). Calibration is the process of adjusting these values to improve their interpretative accuracy [6].
• Process:
  • Use a set of LRs computed from a development dataset (with known ground truth) as the input variable.
  • Use the ground truth (e.g., 1 for same-author, 0 for different-author) as the target variable.
  • Fit a logistic regression model to map the raw LR values to well-calibrated posterior probabilities, which can then be converted back into calibrated LRs [6]. This step ensures that an LR of 10, for instance, truly corresponds to evidence that is ten times more likely under Hp than under Hd.

Phase 4: Performance Assessment and Validation

Objective: To quantitatively evaluate the validity and reliability of the calibrated LRs.

• Metrics:
  • Log-Likelihood-Ratio Cost (Cllr): This is a primary metric for evaluating LR-based systems. It measures the average cost of the LRs across all comparisons, penalizing both misleading evidence (strong LRs for the wrong hypothesis) and uninformative evidence (LRs close to 1). A lower Cllr indicates better performance [6].
  • Tippett Plots: These are cumulative distribution plots that visualize the performance of the LRs. They show the proportion of same-author and different-author comparisons that have an LR greater than or equal to a given value. Tippett plots allow for a quick visual assessment of the method's discrimination and the rate of misleading evidence [6].
  • Integrated Calibration Index (ICI): A numeric measure of calibration performance, defined as the weighted mean absolute difference between observed and predicted probabilities. It explicitly incorporates the distribution of predicted probabilities, providing a single-figure summary of calibration quality. Related metrics E50 and E90 (the median and 90th percentile of absolute differences) offer additional insight [72].

Table 2: Key Performance Metrics for Validating FTC Systems

Metric	Purpose	Interpretation
Cllr (Log-Likelihood-Ratio Cost)	Overall performance measure assessing the accuracy and discriminability of LRs.	Lower values are better. A perfect system has Cllr = 0.
Tippett Plot	Visual assessment of discrimination and rates of misleading evidence.	Clear separation of the same-author and different-author curves is desired.
ICI (Integrated Calibration Index)	Numeric summary of calibration accuracy.	Closer to 0 indicates better agreement between predicted and observed probabilities.
E50 / E90	Percentiles of the absolute calibration error.	Describe the distribution of calibration errors (e.g., median error).

The Scientist's Toolkit: Essential Research Reagents

Table 3: Key Research Reagent Solutions for FTC Validation

Item	Function in FTC Validation	Exemplar / Note
Reference Corpus	Provides a realistic and relevant dataset of textual documents for model training and validation.	Amazon Authorship Verification Corpus (AAVC) [6].
Feature Extraction Algorithm	Converts raw text into quantitative measurements for statistical analysis.	Character n-gram frequency counter; Word frequency model.
Statistical Model for LR	Computes the initial likelihood ratio based on the similarity and typicality of the features.	Dirichlet-Multinomial model [6].
Calibration Model	Adjusts raw LRs to ensure they are statistically coherent and accurately represent the evidence strength.	Logistic Regression Calibrator [6].
Validation Software	Computes performance metrics and generates diagnostic plots to assess system validity.	Software calculating Cllr, ICI [72], and generating Tippett plots [6].

Diagram 2: LR Framework Logic

Validation under realistic casework conditions is not an optional extra but a fundamental requirement for the adoption of forensic text comparison methods in judicial proceedings. By deliberately designing validation studies that incorporate realistic mismatch scenarios, such as differences in topic, and by employing a rigorous statistical framework involving LR calculation and logistic regression calibration, researchers can provide the necessary foundation for scientifically defensible and demonstrably reliable FTC. The protocols outlined herein provide a pathway for researchers to generate robust validation data, thereby strengthening the bridge between forensic linguistics research and its practical application in the legal system.

Conclusion

Logistic-regression calibration provides a mathematically rigorous and forensically sound methodology for converting similarity scores into valid likelihood ratios, directly addressing the need for transparent, reproducible, and bias-resistant practices in forensic text comparison. The successful implementation of this framework hinges on a thorough understanding of the LR foundation, meticulous application of calibration techniques that account for real-world data challenges, and rigorous empirical validation under conditions that mirror actual casework. Future progress in the field depends on the development of more extensive and topic-diverse background databases, the refinement of calibration methods robust to extreme data scarcity, and the widespread adoption of standardized validation protocols as outlined in emerging international standards like ISO 21043. This paradigm shift towards a forensic data science approach is essential for strengthening the scientific foundation of forensic linguistics and ensuring its continued admissibility and reliability in judicial proceedings.

References

• 1. Population Genetics and Statistics for Forensic Analysts [https://nij.ojp.gov/nij-hosted-online-training-courses/population-genetics-and-statistics-forensic-analysts/statistics/logical-approach/likelihood-ratio]
• 2. Validation in Forensic Text Comparison: Issues and ... [https://research.manchester.ac.uk/en/publications/validation-in-forensic-text-comparison-issues-and-opportunities]
• 3. Commentary on: Aggadi N, Zeller K, Busey T. Quantifying ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12584119/]
• 4. Likelihood Ratio as Weight of Forensic Evidence: A Closer Look [https://pmc.ncbi.nlm.nih.gov/articles/PMC7339646/]
• 5. In the context of forensic casework, are there meaningful ... [https://www.sciencedirect.com/science/article/pii/S2589871X21000279]
• 6. Validation in Forensic Text Comparison: Issues and ... [https://www.mdpi.com/2226-471X/9/2/47]
• 7. Strength of linguistic text evidence: A fused forensic ... [https://www.sciencedirect.com/science/article/abs/pii/S0379073817302475]
• 8. A method to validate scoring systems based on logistic ... [https://www.sciencedirect.com/science/article/abs/pii/S0169260720301681]
• 9. A tutorial on calibration measurements and ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC7075534/]
• 10. Calibration: the Achilles heel of predictive analytics [https://bmcmedicine.biomedcentral.com/articles/10.1186/s12916-019-1466-7]
• 11. Evaluation of Forensic Data Using Logistic Regression-Based Classification Methods and an R Shiny Implementation - PMC [https://www.ncbi.nlm.nih.gov/pmc/articles/PMC7609892/]
• 12. Likelihood ratio estimation for authorship text evidence: An empirical comparison of score- and feature-based methods - PubMed [https://pubmed.ncbi.nlm.nih.gov/35334288/]
• 13. Reproducible research practices and transparency across ... [https://escholarship.org/uc/item/6m62j7p6]
• 14. Geoffrey Stewart Morrison [https://geoff-morrison.net/]
• 15. Evaluation of Forensic Data Using Logistic Regression ... [https://www.frontiersin.org/journals/chemistry/articles/10.3389/fchem.2020.00738/full]
• 16. Replicability of simulation studies for the investigation ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC10791519/]
• 17. Replication in Scientific Validation and Identification of ... [https://asatonline.org/for-parents/becoming-a-savvy-consumer/role-of-replication-in-scientific-validation/]
• 18. Why is Replication in Research Important? [https://www.aje.com/arc/why-is-replication-in-research-important]
• 19. Empirical validation of an automated approach to data use ... [https://www.sciencedirect.com/science/article/pii/S2666979X21000380]
• 20. Empirical evaluation of internal validation methods for ... [https://bmcmedresmethodol.biomedcentral.com/articles/10.1186/s12874-023-01844-5]
• 21. Evaluation of Forensic Data Using Logistic Regression ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC7609892/]
• 22. An overview of log likelihood ratio cost in forensic science [https://pmc.ncbi.nlm.nih.gov/articles/PMC11031735/]
• 23. Validation in Forensic Text Comparison: Issues and ... [https://www.bohrium.com/paper-details/validation-in-forensic-text-comparison-issues-and-opportunities/959270185368289283-39292]
• 24. Score based procedures for the calculation of forensic ... [https://www.sciencedirect.com/science/article/pii/S1355030617300849]
• 25. Tutorial on logistic-regression calibration and fusion [https://ui.adsabs.harvard.edu/abs/2021arXiv210408846M/abstract]
• 26. 1.16. Probability calibration [https://scikit-learn.org/stable/modules/calibration.html]
• 27. Mitigating Algorithmic Bias Through Probability Calibration [https://www.mdpi.com/2227-7390/13/13/2183]
• 28. Bias, Calibration and Stability in Logistic Regression Models [https://rsisinternational.org/journals/ijrias/articles/bias-calibration-and-stability-in-logistic-regression-models-a-comparative-simulation-study-of-mle-firth-and-ridge-methods/]
• 29. Do you know when to use Calibrated Cross Validation for ... [https://medium.com/chat-gpt-now-writes-all-my-articles/do-you-know-when-to-use-calibrated-cross-validation-for-ml-models-d62c73e018f4]
• 30. Why do we need separate data for probability calibration? [https://stats.stackexchange.com/questions/605252/why-do-we-need-separate-data-for-probability-calibration]
• 31. Training-validation-test split and cross-validation done right [https://www.machinelearningmastery.com/training-validation-test-split-and-cross-validation-done-right/]
• 32. A Comprehensive Guide on Model Calibration [https://towardsdatascience.com/a-comprehensive-guide-on-model-calibration-part-1-of-4-73466eb5e09a/]
• 33. CalibratedClassifierCV [https://scikit-learn.org/stable/modules/generated/sklearn.calibration.CalibratedClassifierCV.html]
• 34. Train-val-test splits and cross-validation [https://medium.com/@masadeghi6/how-to-split-your-data-for-machine-learning-eae893a8799c]
• 35. When to do the split training and test set - Cross Validated [https://stats.stackexchange.com/questions/239381/when-to-do-the-split-training-and-test-set]
• 36. Validation in Forensic Text Comparison: Issues and ... [https://doaj.org/article/001314fb2a6f451db8d5c6556cf8233a]
• 37. A Threshold & Calibration Deep Dive in LR [https://www.numberanalytics.com/blog/lr-threshold-calibration-deep-dive]
• 38. The Million Authors Corpus: A Cross-Lingual and ... [https://aclanthology.org/2025.findings-acl.1335/]
• 39. Posterior probability [https://en.wikipedia.org/wiki/Posterior_probability]
• 40. Why is logistic well regression , and how to ruin its... calibrated [https://stats.stackexchange.com/questions/390487/why-is-logistic-regression-well-calibrated-and-how-to-ruin-its-calibration]
• 41. (PDF) Evaluation of Forensic Data Using Logistic -Based... Regression [https://www.academia.edu/144576376/Evaluation_of_Forensic_Data_Using_Logistic_Regression_Based_Classification_Methods_and_an_R_Shiny_Implementation]
• 42. A guide to ISO 21043 Forensic Sciences from the ... [https://www.sciencedirect.com/science/article/pii/S1355030625000887]
• 43. AI Training Data Solutions: What's Changing in 2025? [http://macgence.com/blog/ai-training-data-solutions-whats-changing-in-2025/]
• 44. From Data Scarcity to Solutions: Hydrological and Water ... [https://www.mdpi.com/2073-4441/17/6/823]
• 45. Synthetic data for ML: the game-changer in training for 2025 [https://cleverx.com/blog/synthetic-data-for-ml-the-game-changer-in-training-for-2025]
• 46. The Future of Artificial Intelligence in the Face of Data ... [https://www.sciencedirect.com/org/science/article/pii/S1546221825005375]
• 47. Natural Language Processing Techniques in 2025 [https://labelyourdata.com/articles/natural-language-processing/techniques]
• 48. Evaluation of Forensic Data Using Logistic Regression ... [https://www.frontiersin.org/articles/10.3389/fchem.2020.00738/full]
• 49. Logistic Regression: The Myth of Natural Calibration [https://valeman.medium.com/logistic-regression-the-myth-of-natural-calibration-a7496237bc70]
• 50. From Logistic Regression to Foundation Models [https://pubmed.ncbi.nlm.nih.gov/41245920/]
• 51. From Logistic Regression to Foundation Models [https://pmc.ncbi.nlm.nih.gov/articles/PMC12611635/]
• 52. Calibration-Aware Scoring [https://www.emergentmind.com/topics/calibration-aware-scoring]
• 53. In the context of forensic casework, are there meaningful metrics of the degree of calibration? - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC8212664/]
• 54. Tutorial on logistic-regression calibration and fusion [https://research.aston.ac.uk/en/publications/tutorial-on-logistic-regression-calibration-and-fusion-converting/]
• 55. Calibration and Validation - Forensic Data Science Laboratory [https://forensic-data-science.net/calibration-and-validation/]
• 56. Calibration Techniques and it’s importance in Machine Learning | Medium [https://kingsubham27.medium.com/calibration-techniques-and-its-importance-in-machine-learning-71bec997b661]
• 57. The Complete Guide to Platt Scaling [https://www.blog.trainindata.com/complete-guide-to-platt-scaling/]
• 58. Smooth Isotonic Regression: A New Method to Calibrate ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC3248752/]
• 59. fastml.com/classifier-calibration-with- platts - scaling -and- isotonic ... [http://fastml.com/classifier-calibration-with-platts-scaling-and-isotonic-regression/]
• 60. Platt Scaling for Model Calibration: A Visual Guide [https://blog.dailydoseofds.com/p/platt-scaling-for-model-calibration]
• 61. Trier of Fact | Burger Law [https://mccreadylaw.com/legal-terms/trier-of-fact/]
• 62. trier of fact | Wex | US Law | LII / Legal Information Institute [https://www.law.cornell.edu/wex/trier_of_fact]
• 63. Trier of fact [https://en.wikipedia.org/wiki/Trier_of_fact]
• 64. An overview of log likelihood ratio cost in forensic science [https://www.sciencedirect.com/science/article/pii/S2589871X24000135]
• 65. Strength of forensic text comparison evidence from stylometric ... [https://researchportalplus.anu.edu.au/en/publications/strength-of-forensic-text-comparison-evidence-from-stylometric-fe/]
• 66. An overview of log likelihood ratio cost in forensic science [https://pubmed.ncbi.nlm.nih.gov/38645839/]
• 67. Consensus on validation of forensic voice comparison [https://www.sciencedirect.com/science/article/pii/S1355030621000083]
• 68. Graphical assessment of internal and external calibration of ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC4793659/]
• 69. Likelihood ratio data to report the validation of a forensic ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC5144651/]
• 70. Bio-Metrics [https://oxfordwaveresearch.com/products/bio-metrics/]
• 71. Score-based likelihood ratios for linguistic text evidence ... [https://www.sciencedirect.com/science/article/abs/pii/S0379073821003005]
• 72. The Integrated Calibration Index (ICI) and related metrics for ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC6771733/]